题目内容
已知g(x)=lnx,其导函数为g'(x),反函数为g-1(x)
(1)求证:y=x+1的函数图象恒不在y=g-1(x)的函数图象的上方.
(2)设函数f(x)=eg(x)-g'(x)-a•g(x)(a∈R).若f(x)有两个极值点x1,x2;记过点A(x1,f(x1))B(x2,f(x2))的直线斜率为k.问:是否存在a,使得k=2-a?若存在,求出a的值;若不存在,请说明理由.
(3)求证:
(
)n<
.(n∈N*)
(1)求证:y=x+1的函数图象恒不在y=g-1(x)的函数图象的上方.
(2)设函数f(x)=eg(x)-g'(x)-a•g(x)(a∈R).若f(x)有两个极值点x1,x2;记过点A(x1,f(x1))B(x2,f(x2))的直线斜率为k.问:是否存在a,使得k=2-a?若存在,求出a的值;若不存在,请说明理由.
(3)求证:
| n |
 |
| k=1 |
| k |
| n |
| e |
| e-1 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)设令h(x)=g-1(x)-x-1=ex-x-1,判断函数h(x)的单调性,根据单调性得到h(x)≥h(0)=0,问题得以解决.
(2)先求导,再构造函数F(x)=x2-ax+1,然后再分类讨论函数的单调性,利用斜率公式表示出k=
,再假设存在a的值,使得k=2-a,导代入转化为
亦即x2-
-2lnx2=0,x2>1,设h(t)=t-
-2lnt,t>1,根据函数的单调性,得出矛盾,问题得以解决.
(3)由(1)有1+x≤ex(当且仅当x=0时取等)对任意的实数R均成立,利用放缩法来证明,
(2)先求导,再构造函数F(x)=x2-ax+1,然后再分类讨论函数的单调性,利用斜率公式表示出k=
| f(x1)-f(x2) |
| x1-x2 |
亦即x2-
| 1 |
| x2 |
| 1 |
| t |
(3)由(1)有1+x≤ex(当且仅当x=0时取等)对任意的实数R均成立,利用放缩法来证明,
解答:
解(1)∵g(x)=lnx,其导函数为g'(x),反函数为g-1(x),
令h(x)=g-1(x)-x-1=ex-x-1,
∴h'(x)=ex-1,
令h'(x)=ex-1=0,即x=0,
∴h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴h(x)≥h(0)=0,从而所得结论成立.
(2)∵f(x)=eg(x)-g'(x)-a•g(x)(a∈R).
∴f(x)=x-
-alnx,f(x)的定义域为(0,+∞),
∴f′(x)=1+
-
=
,
令F(x)=x2-ax+1,其判别式△=a2-4,
从而当|a|≤2时,△≤0,故f′(x)≥0,故f(x)在(0,+∞)上单调递增.
当a<-2时,△>0,故F(x)=0的两根都小于0,在(0,+∞)上,f′(x)>0,故f(x)在(0,+∞)上单调递增.
当当a>2时,△>0,故F(x)=0的两根为x1=
(a-
),x2=
(a+
),
当0<x<x1时,f′(x)>0;当x1,<x<x2时,f′(x)<0;当x>x2时,f′(x)>0,
故f(x)分别在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.
从而当a>2是,函数有两个极值点.
又因为f(x1)-f(x2)=(x1-x2)+
-a(lnx1-lnx2),
所以k=
=1+
-a
又由(1)知,x1x2=1.于是k=2-a
若存在a,使得k=2-a则
=1.即lnx1-lnx2=x1-x2,.
亦即x2-
-2lnx2=0,x2>1(*)
令h(t)=t-
-2lnt,t>1,
再由(*)知,函数h(t)=t-
-2lnt在(0,+∞)上单调递增,而x2>1,
所以x2-
-2lnx2>1-
-2ln1=0,这与(*)式矛盾.故不存在a,使得k=2-a,
(3)由(1)有1+x≤ex(当且仅当x=0时取等)对任意的实数R均成立,
令x=-
(n∈N*,i=1,2,3,…,n-1),则1-
<e-
,
,
,
∴
(
)n=(
)n+(
)n+…+(
)n+(
)n<e-(n-1)+e-(n-2)+…+e-1+1,
∵e-(n-1)+e-(n-2)+…+e-1+1=
<
=
,
从而结论成立.
令h(x)=g-1(x)-x-1=ex-x-1,
∴h'(x)=ex-1,
令h'(x)=ex-1=0,即x=0,
∴h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴h(x)≥h(0)=0,从而所得结论成立.
(2)∵f(x)=eg(x)-g'(x)-a•g(x)(a∈R).
∴f(x)=x-
| 1 |
| x |
∴f′(x)=1+
| 1 |
| x2 |
| a |
| x |
| x2-ax+1 |
| x2 |
令F(x)=x2-ax+1,其判别式△=a2-4,
从而当|a|≤2时,△≤0,故f′(x)≥0,故f(x)在(0,+∞)上单调递增.
当a<-2时,△>0,故F(x)=0的两根都小于0,在(0,+∞)上,f′(x)>0,故f(x)在(0,+∞)上单调递增.
当当a>2时,△>0,故F(x)=0的两根为x1=
| 1 |
| 2 |
| a2-4 |
| 1 |
| 2 |
| a2-4 |
当0<x<x1时,f′(x)>0;当x1,<x<x2时,f′(x)<0;当x>x2时,f′(x)>0,
故f(x)分别在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.
从而当a>2是,函数有两个极值点.
又因为f(x1)-f(x2)=(x1-x2)+
| x1-x2 |
| x1x2 |
所以k=
| f(x1)-f(x2) |
| x1-x2 |
| 1 |
| x1x2 |
| lnx1-lnx2 |
| x1-x2 |
又由(1)知,x1x2=1.于是k=2-a
| lnx1-lnx2 |
| x1-x2 |
若存在a,使得k=2-a则
| lnx1-lnx2 |
| x1-x2 |
亦即x2-
| 1 |
| x2 |
令h(t)=t-
| 1 |
| t |
再由(*)知,函数h(t)=t-
| 1 |
| t |
所以x2-
| 1 |
| x2 |
| 1 |
| 1 |
(3)由(1)有1+x≤ex(当且仅当x=0时取等)对任意的实数R均成立,
令x=-
| i |
| n |
| i |
| n |
| i |
| n |
|
|
∴
| n |
 |
| i=1 |
| k |
| n |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| n |
| n |
∵e-(n-1)+e-(n-2)+…+e-1+1=
| 1-e-n |
| 1-e-1 |
| 1 |
| 1-e-1 |
| e |
| e-1 |
从而结论成立.
点评:本题考查了导数与函数的单调性和极值的关系,以及直线的斜率,不等式的证明,培养了学生的转化能力,计算能力,计算量比较大,思考有一定的难度,属于难题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
用平行于圆锥底面的平面截圆锥,所得截面面积与底面面积的比是1:3,这截面把圆锥母线分成的两段的比是( )
| A、1:3 | ||
B、1:(
| ||
| C、1:9 | ||
D、
|
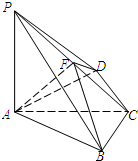 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.