题目内容
3．
设全集U是实数集R，M={x|x2＞4}，N为函数y=ln（4x-3-x2）的定义域，则图中阴影部分所表示的集合是{x|1＜x≤2}．
分析 由图象可知阴影部分对应的集合为N∩（∁UM），然后根据集合的基本运算即可．
解答 解：M={x|x2＞4}={x|x＞2或x＜-2}，
由4x-3-x2＞0，得1＜x＜3，即N={x|1＜x＜3}，
由图象可知阴影部分对应的集合为N∩（∁UM），
∴∁UM={x|-2≤x≤2}，
∴N∩（∁UM）={x|1＜x≤2}；
故答案为：{x|1＜x≤2}．
点评 本题主要考查集合的基本运算，利用Venn图确定集合的关系是解决本题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
13．为得到函数$y=2sin（2x+\frac{π}{4}）$的图象，只需将函数y=2cos2x的图象（ ）
| A． | 向左平移$\frac{π}{4}$单位 | B． | 向右平移$\frac{π}{4}$单位 | C． | 向左平移$\frac{π}{8}$单位 | D． | 向右平移$\frac{π}{8}$单位 |
14．若集合M={x|1＜x＜4}，N={x|x2-7x＜0}，则M∩N等于（ ）
| A． | {x|0＜x＜4} | B． | {x|1＜x＜7} | C． | {x|1＜x＜4} | D． | {x|4＜x＜7} |
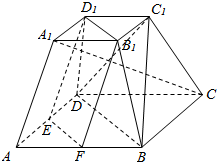如图，在正四棱台ABCD-A1B1C1D1中，A1B1=a，AB=2a，E、F分别是AD、AB的中点．求证：平面EFB1D1∥平面BDC1．