题目内容
11.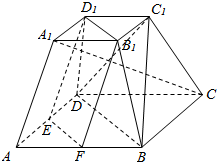 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,E、F分别是AD、AB的中点.求证:平面EFB1D1∥平面BDC1.
分析 证明平面EFB1D1∥平面BDC1,可采用面面平行的判定定理,连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P得到BD∥平面EFB1D1.然后证明PN∥MC1,则由面面平行的判定定理得答案.
解答  证明:连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
证明:连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
由题意,BD∥B1D1,
∵BD?平面EFB1D1,B1D1?平面EFB1D1,∴BD∥平面EFB1D1,
又∵A1B1=a,AB=2a,∴$M{C_1}=\frac{1}{2}{A_1}{C_1}=\frac{{\sqrt{2}}}{2}a$.
又∵E、F分别是AD、AB的中点,
∴$NP=\frac{1}{4}AC=\frac{{\sqrt{2}}}{2}a$.
∴MC1=NP.
又∵AC∥A1C1,∴MC1∥NP.
∴四边形MC1PN为平行四边形.
∴PC1∥MN.
∵PC1?平面EFB1D1,MN?平面EFB1D1,∴PC1∥平面EFB1D1
∵PC1∩BD=P,∴平面EFB1D1∥平面BDC1.
点评 本题考查面面平行的判定,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
16.设复数z=3+i,且iz=a+bi(a,b∈R),则a+b等于( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
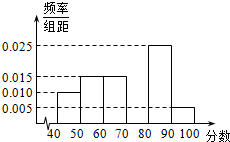 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题: 设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.