题目内容
18.已知三棱锥A-BCD中,AB=CD,且直线AB与CD成60°角,点M、N分别是BC、AD的中点,求直线AB和MN所成的角.分析 取AC的中点P,连结PM、PN,则∠MPN为AB与CD所成的角(或所成的角的补角),∠PMN是AB与MN所成的角(或所成角的补角),由此能求出直线AB与MN所成的角.
解答 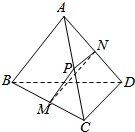 解:如图,取AC的中点P,连结PM、PN,
解:如图,取AC的中点P,连结PM、PN,
则PM∥AB,且PM=$\frac{1}{2}AB$,PN∥CD,且PN=$\frac{1}{2}CD$,
∴∠MPN为AB与CD所成的角(或所成的角的补角),
∴∠MPN=60°或∠MPN=120°,
若∠MPN=60°,∵PM∥AB,∴∠PMN是AB与MN所成的角(或所成角的补角),
又∵AB=CD,∴PM=PN《
∴△PMN是等边三角形,∴∠PMN=60°,
∴AB与MN所成的角为60°;
若∠MPN=120°,则△PMN是等腰三角形,∴∠PMN=30°,
∴AB与MN所成的角为30°,
∴直线AB与MN所成的角为60°或30°.
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
8.已知$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$,且$\overrightarrow{AC}=\overrightarrow a$,$\overrightarrow{BD}=\overrightarrow b$,则$\overrightarrow{AB}$=( )
| A. | $\frac{1}{2}(\overrightarrow a-\overrightarrow b)$ | B. | $\frac{1}{2}(\overrightarrow a+\overrightarrow b)$ | C. | $\frac{1}{2}(\overrightarrow b-\overrightarrow a)$ | D. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
13.等比数列{an}的公比为2,且a3a11=16,则a5=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±2 |
10.在极坐标系中,设圆C:ρ=4cosθ与直线l:θ=$\frac{π}{4}$(ρ∈R)交于A,B两点,求以AB为直径的圆的极坐标方程为( )
| A. | ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$) | B. | ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}$) | C. | ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$) | D. | ρ=-2$\sqrt{2}$cos(θ-$\frac{π}{4}$) |
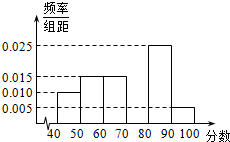 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题: 设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.