题目内容
15.平面直角坐标系xOy中,曲线C1上的动点M到点F(0,1)的距离比它到x轴的距离大1.(1)求曲线C1方程;
(2)设P为C1上一点(位于y轴右侧),过P作C1的切线,与x轴交于A.直线AB与圆C2:x2+(y-1)2=1相切于点B(异于点O),问△PAB与△PAO的面积之比是否为定值?若是,求出该比值;若不是,说明理由.
分析 (1)利用曲线C1上的动点M到点F(0,1)的距离与它到y=-1的距离相等,可知曲线C1是以F(0,1)为焦点,开口向上的抛物线,进而计算即得结论;
(2)通过设P(x0,$\frac{1}{4}$${{x}_{0}}^{2}$),进而计算出切线AP方程为y=$\frac{{x}_{0}}{2}$x-$\frac{1}{4}$${{x}_{0}}^{2}$,并令y=0可知A($\frac{1}{2}$x0,0),通过设圆C2的切线AB的方程为x=ty+$\frac{1}{2}$x0,利用1=$\frac{|0-t-\frac{1}{2}{x}_{0}|}{\sqrt{1+{t}^{2}}}$可知圆C2的切线AB的方程为x=$\frac{4-{{x}_{0}}^{2}}{4{x}_{0}}$y+$\frac{1}{2}$x0,利用圆外一点切线的性质计算可知dAB=yP,进而可得结论.
解答  解:(1)∵曲线C1上的动点M到点F(0,1)的距离比它到x轴的距离大1,
解:(1)∵曲线C1上的动点M到点F(0,1)的距离比它到x轴的距离大1,
∴曲线C1上的动点M到点F(0,1)的距离与它到y=-1的距离相等,
∴曲线C1是以F(0,1)为焦点,开口向上的抛物线,
∴曲线C1方程为:x2=4y;
(2)结论:△PAB与△PAO的面积相等.
理由如下:
设P(x0,$\frac{1}{4}$${{x}_{0}}^{2}$),则过点P的曲线C1的切线的斜率为$\frac{1}{2}$x0,
则切线AP方程为:y=$\frac{{x}_{0}}{2}$x-$\frac{1}{4}$${{x}_{0}}^{2}$,
令y=0可知x=$\frac{1}{2}$x0,即A($\frac{1}{2}$x0,0),
设圆C2的切线AB的方程为:x=ty+$\frac{1}{2}$x0,
则1=$\frac{|0-t-\frac{1}{2}{x}_{0}|}{\sqrt{1+{t}^{2}}}$,整理得:t=$\frac{1}{{x}_{0}}$-$\frac{{x}_{0}}{4}$,
∴圆C2的切线AB的方程为:x=$\frac{4-{{x}_{0}}^{2}}{4{x}_{0}}$y+$\frac{1}{2}$x0,
点P到直线AB的距离dAB=$\frac{|{x}_{0}+(\frac{{x}_{0}}{4}-\frac{1}{{x}_{0}})•\frac{1}{4}{{x}_{0}}^{2}-\frac{1}{2}{x}_{0}|}{\sqrt{1+(\frac{{x}_{0}}{4}-\frac{1}{{x}_{0}})^{2}}}$=$\frac{|\frac{{{x}_{0}}^{3}+4{x}_{0}}{16}|}{\sqrt{\frac{1}{2}+\frac{{{x}_{0}}^{2}}{16}+\frac{1}{{{x}_{0}}^{2}}}}$=$\frac{1}{4}$${{x}_{0}}^{2}$,
又∵AB=OA,dAB=yP,
∴△PAB与△PAO的面积相等.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$) | B. | ρ=2$\sqrt{2}$sin(θ-$\frac{π}{4}$) | C. | ρ=2$\sqrt{2}$cos(θ+$\frac{π}{4}$) | D. | ρ=-2$\sqrt{2}$cos(θ-$\frac{π}{4}$) |
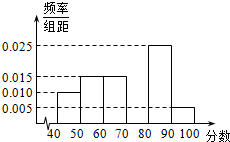 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(满分100分,均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.根据图形的信息,回答下列问题: 设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N为函数y=ln(4x-3-x2)的定义域,则图中阴影部分所表示的集合是{x|1<x≤2}.