题目内容
过点A(4,-2)任作一条直线l与抛物线y2=2x交于不同的两点P,Q,问:抛物线y2=2x上是否存在点B,使∠PBQ总等于90°?
考点:直线与圆锥曲线的关系
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:假设抛物线y2=2x上存在点B,使∠PBQ总等于90°.设出直线方程联立抛物线方程,消去x,得到y的方程,设B(x0,y0),P(x1,y1),Q(x2,y2),运用韦达定理和直线的斜率公式,结合两直线垂直的条件,化简整理,得到2m(y0-2)+y02-4=0,再由恒等式知识即可求得B的坐标.
解答:
解:假设抛物线y2=2x上存在点B,使∠PBQ总等于90°.
设直线l:x-4=m(y+2),
与抛物线y2=2x联立,消去x,得y2-2my-4(m+2)=0,
设B(x0,y0),P(x1,y1),Q(x2,y2),
y1+y2=2m,y1y2=-4(2+m),①
kPB=
=
=
,
kQB=
=
=
,
由于∠PBQ=90°,则PB⊥QB,
即有kPB•kQB=-1,
得y1y2+y0(y1+y2)+y02=-4,
将①代入得,2m(y0-2)+y02-4=0,
当y0=2时,上式恒成立 此时x0=2,
所以抛物线y2=2x上存在点B(2,2),使∠PBQ总等于90°.
设直线l:x-4=m(y+2),
与抛物线y2=2x联立,消去x,得y2-2my-4(m+2)=0,
设B(x0,y0),P(x1,y1),Q(x2,y2),
y1+y2=2m,y1y2=-4(2+m),①
kPB=
| y1-y0 |
| x1-x0 |
| y1-y0 | ||
|
| 2 |
| y1+y0 |
kQB=
| y2-y0 |
| x2-x0 |
| y2-y0 | ||
|
| 2 |
| y2+y0 |
由于∠PBQ=90°,则PB⊥QB,
即有kPB•kQB=-1,
得y1y2+y0(y1+y2)+y02=-4,
将①代入得,2m(y0-2)+y02-4=0,
当y0=2时,上式恒成立 此时x0=2,
所以抛物线y2=2x上存在点B(2,2),使∠PBQ总等于90°.
点评:本题考查抛物线的方程和运用,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理和直线的斜率公式,考查两直线垂直的条件,考查恒成立问题注意运用恒等式的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从数字1,2,3,…,10中,按由小到大的顺序取出a1、a2、a3,且a2-a1≥2,a3-a2≥2,则不同的取法有( )
| A、20种 | B、35种 |
| C、56种 | D、60种 |
设集合A={x||x-2|≤2},B={x|
>1},则∁R(A∩B)等于( )
| x |
| x+1 |
| A、{x|0≤x≤4} | B、R |
| C、{x|x<-1} | D、∅ |
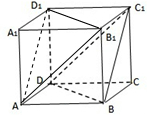 如图,正方体ABCD-A1B1C1D1.
如图,正方体ABCD-A1B1C1D1.