题目内容
已知函数f（x）=xlnx+2xf′（1），试比较f（e）与f（1）的大小关系．
考点：导数的运算
专题：导数的概念及应用
分析：通过求导先求出f′（1），得到函数f（x）的表达式，再将x=e，x=1代入表达式，从而比较f（e），f（1）的大小．
解答：
解：由题意得f′（x）=1+lnx+2f′（1），
令x=1得f′（1）=1+ln1+2f′（1）即f′（1）=-1，
所以f（x）=xlnx-2x，
所以f（e）=elne-2e=-e，f（1）=-2，
得f（e）＜f（1）．
令x=1得f′（1）=1+ln1+2f′（1）即f′（1）=-1，
所以f（x）=xlnx-2x，
所以f（e）=elne-2e=-e，f（1）=-2，
得f（e）＜f（1）．
点评：本题考查了导数的应用，考查了函数求值问题，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
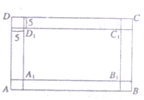某市政府为了打造宜居城市，计划在公园内新建一个如图所示的矩形ABCD的休闲区，内不是矩形景观区A1B1C1D1，景观区四周是人行道，已知景观区的面积为8000平方米，人行道的宽为5米（如图所示）．已知直线3x+4y-3=0与直线6x+my+14=0平行，则它们之间的距离是（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知直线l过点P（3，2）．复数z=
在复平面内对应的点在（ ）
| 1+i |
| i2015 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |