题目内容
5.己知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),以C的一个顶点为圆心,a为半径的圆被C截得的劣弧长为$\frac{2π}{3}a$,则双曲线C的离心率为$\frac{2\sqrt{10}}{5}$.分析 设双曲线与圆A在第一象限的交点为P,由题意可得AP与x轴的夹角为60°,由三角函数的定义可得P的坐标,代入双曲线的方程,结合a,b,c和离心率公式计算即可得到所求值.
解答 解:设双曲线与圆A在第一象限的交点为P,
由题意可得AP与x轴的夹角为60°,
即有P(a+acos60°,asin60°),
即为($\frac{3a}{2}$,$\frac{\sqrt{3}}{2}$a),
代入双曲线的方程可得$\frac{9{a}^{2}}{4{a}^{2}}$-$\frac{3{a}^{2}}{4{b}^{2}}$=1,
即有3a2=5b2=5(c2-a2),
即5c2=8a2,
由e=$\frac{c}{a}$,可得e=$\frac{2\sqrt{10}}{5}$.
故答案为:$\frac{2\sqrt{10}}{5}$.
点评 本题考查双曲线的离心率的求法,注意运用点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
17.某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如表:
由于部分数据丢失,只知道从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$.
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
17.平面直角坐标系xOy中,双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线C2:y2=2px(p>0)交于点O,A,B,若△OAB的重心为C2的焦点,则C1的渐近线方程为( )
| A. | y=±$\frac{\sqrt{6}}{4}$x | B. | y=±$\frac{2\sqrt{6}}{3}$x | C. | y=±2$\sqrt{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
14.已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左右焦点分别为F1、F2,点P为双曲线上一点,△F1PF2的内切圆圆心为M,若S${\;}_{△{F}_{1}PM}$=S${\;}_{△{F}_{2}PM}$+8,那么S${\;}_{△{F}_{1}M{F}_{2}}$( )
| A. | 2$\sqrt{7}$ | B. | 6 | C. | 8 | D. | 10 |
20.已知点F1、F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )
| A. | (1,+∞) | B. | [$\frac{\sqrt{10}}{2}$,+∞) | C. | (1,$\frac{\sqrt{10}}{2}$] | D. | (1,$\frac{5}{2}$] |
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
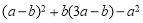 ,其中
,其中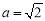 ,
,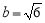 .
.