题目内容
20.已知点F1、F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )| A. | (1,+∞) | B. | [$\frac{\sqrt{10}}{2}$,+∞) | C. | (1,$\frac{\sqrt{10}}{2}$] | D. | (1,$\frac{5}{2}$] |
分析 由直角三角形的判定定理可得△PF1F2为直角三角形,且PF1⊥PF2,运用双曲线的定义,可得|PF1|-|PF2|=2a,
又|PF1|≥3|PF2|,可得|PF2|≤a,再由勾股定理,即可得到c≤$\frac{\sqrt{10}}{2}$a,运用离心率公式,即可得到所求范围.
解答 解:由|F1F2|=2|OP|,可得|OP|=c,
即有△PF1F2为直角三角形,且PF1⊥PF2,
可得|PF1|2+|PF2|2=|F1F2|2,
由双曲线定义可得|PF1|-|PF2|=2a,
又|PF1|≥3|PF2|,可得|PF2|≤a,
即有(|PF2|+2a)2+|PF2|2=4c2,
化为(|PF2|+a)2=2c2-a2,
即有2c2-a2≤4a2,
可得c≤$\frac{\sqrt{10}}{2}$a,
由e=$\frac{c}{a}$可得
1<e≤$\frac{\sqrt{10}}{2}$,
故选:C.
点评 本题考查双曲线的离心率的范围,注意运用双曲线的定义和直角三角形的性质,考查运算能力,属于中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
12.执行如图所示的程序框图,若依次输入m=${0.6^{\frac{1}{2}}}$,n=0.6-2,p=${({\frac{1}{3}})^{\frac{1}{2}}}$,则输出的结果为( )
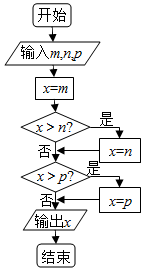

| A. | ${({\frac{1}{3}})^{\frac{1}{2}}}$ | B. | ${0.6^{\frac{1}{2}}}$ | C. | 0.6-2 | D. | ${0.6^{-\frac{3}{2}}}$ |
7.若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),${a}_{n+1}=\left\{\begin{array}{l}{{a}_{n}-1,{a}_{n}>1}\\{\frac{1}{{a}_{n}},0<{a}_{n}≤1}\end{array}\right.$,若a3=4,则m的所有可能取值为( )
| A. | {6,$\frac{5}{4}$} | B. | {6,$\frac{5}{4}$,$\frac{2}{5}$} | C. | {6,$\frac{5}{4}$,$\frac{1}{5}$} | D. | {6,$\frac{1}{5}$} |
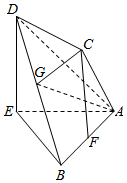 如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.
如图,异面直线AB,CD互相垂直,CF是它们的公垂线段,且F为AB的中点,作DE$\stackrel{∥}{=}$CF,连接AC、BD,G为BD的中点,AB=AC=AE=BE=2.