题目内容
已知点G是斜△ABC的重心，且AG⊥BG，
+
=
，则实数λ的值为 ．
| 1 |
| tanA |
| 1 |
| tanB |
| λ |
| tanC |
考点：正弦定理,余弦定理
专题：三角函数的求值
分析：首先根据三角形的重心性质及直角三角形的斜边的中线等于斜边的一半，得到CD=
AB，再应用余弦定理推出AC2+BC2=5AB2，将
+
=
应用三角恒等变换公式化简得λ=
，然后运用正弦定理和余弦定理，结合前面的结论，即可求出实数λ的值．
| 3 |
| 2 |
| 1 |
| tanA |
| 1 |
| tanB |
| λ |
| tanC |
| sin2C |
| sinAsinBcosC |
解答：
解：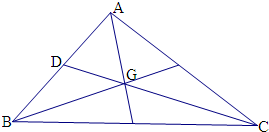
如图，连接CG，延长交AB于D，
由于G为重心，故D为中点，
∵AG⊥BG，∴DG=
AB，
由重心的性质得，CD=3DG，即CD=
AB，
由余弦定理得，AC2=AD2+CD2-2AD•CD•cos∠ADC，
BC2=BD2+CD2-2BD•CD•cos∠BDC，
∵∠ADC+∠BDC=π，AD=BD，
∴AC2+BC2=2AD2+2CD2，
∴AC2+BC2=
AB2+
AB2=5AB2，
又∵
+
=
，
∴
+
=
，
则λ=
=
=
=
=
=
=
．
故答案为：
如图，连接CG，延长交AB于D，由于G为重心，故D为中点，
∵AG⊥BG，∴DG=
| 1 |
| 2 |
由重心的性质得，CD=3DG，即CD=
| 3 |
| 2 |
由余弦定理得，AC2=AD2+CD2-2AD•CD•cos∠ADC，
BC2=BD2+CD2-2BD•CD•cos∠BDC，
∵∠ADC+∠BDC=π，AD=BD，
∴AC2+BC2=2AD2+2CD2，
∴AC2+BC2=
| 1 |
| 2 |
| 9 |
| 2 |
又∵
| 1 |
| tanA |
| 1 |
| tanB |
| λ |
| tanC |
∴
| cosA |
| sinA |
| cosB |
| sinB |
| λcosC |
| sinC |
则λ=
| (sinAcosB+cosAsinB)sinC |
| sinAsinBcosC |
| sin(A+B)sinC |
| sinAsinBcosC |
| sin2C |
| sinAsinBcosC |
| AB2 |
| BC•AC•cosC |
| 2AB2 |
| BC2+AC2-AB2 |
| 2AB2 |
| 4AB2 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：此题考查了正弦、余弦定理，三角形的重心性质，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
如图所示，程序框图（算法流程图）的输出结果是（ ）
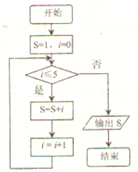
| A、11 | B、15 | C、16 | D、22 |