题目内容
已知a,b,c均为大于-1的实数,且a+b+2c=1,设
+
+
的最大值为m,求不等式|
x|-m|x-3|>0中x的取值范围.
| a+1 |
| b+1 |
| c+1 |
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:根据条件利用柯西不等式求得 (
+
+
)2≤
,可得m=
.不等式即|
x|-
|x-3|>0,即|2x|>5|x-3|,平方,解一元二次不等式,求得x的范围.
| a+1 |
| b+1 |
| c+1 |
| 25 |
| 2 |
5
| ||
| 2 |
| 2 |
5
| ||
| 2 |
解答:
解:∵a+b+2c=1,∴(
+
+
)2=(
+
+
)2≤(a+1+b+1+2c+2)(1+1+
)=
,
当且仅当a+1=b+1=c+1时,等号成立,故m=
=
.
不等式|
x|-m|x-3|>0,即 不等式|
x|-
|x-3|>0,即|2x|>5|x-3|,
平方可得 21x2-150x+225<0,求得
<x<5.
| a+1 |
| b+1 |
| c+1 |
| a+1 |
| b+1 |
| ||
| 2 |
| 2c+2 |
| 1 |
| 2 |
| 25 |
| 2 |
当且仅当a+1=b+1=c+1时,等号成立,故m=
|
5
| ||
| 2 |
不等式|
| 2 |
| 2 |
5
| ||
| 2 |
平方可得 21x2-150x+225<0,求得
| 15 |
| 7 |
点评:本题主要考查柯西不等式的应用,绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
若loga
<1(a>0,a≠1),则实数a的取值范围是( )
| 1 |
| 3 |
| A、(1,+∞) | ||
B、(
| ||
C、(0,
| ||
D、(0,
|
已知集合A={x|y=
-
},则B={x|x≤6},则A∩B等于( )
| x-2 |
| 8-x |
| A、[2,6) |
| B、[2,6] |
| C、[2,8] |
| D、(-∞,6] |
幂函数f(x)的图象过点(3,
),则f(x)的解析式是( )
| 4 | 27 |
A、f(x)=
| |||
B、f(x)=
| |||
C、f(x)=
| |||
D、f(x)=
|
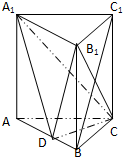 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.