题目内容
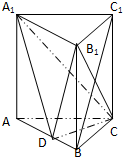已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，AC=BC，点D是AB的中点．（Ⅰ）求证：BC1∥平面CA1D；
（Ⅱ）若底面ABC为边长为2的正三角形，BB1=
| 3 |
考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：（1）连接AC1交A1C于点E，连接DE，只要证明DE∥BC1；
（2）求出CD⊥面AA1B1B，得到CD是棱锥的高，利用棱锥的体积公式解答．
（2）求出CD⊥面AA1B1B，得到CD是棱锥的高，利用棱锥的体积公式解答．
解答：
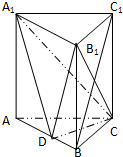（Ⅰ）证明：连接AC1交A1C于点E，连接DE
因为四边形AA1C1C是矩形，则E为AC1的中点
又D是AB的中点，DE∥BC1，
又DE?面CA1D，BC1?面CA1D，
所以BC1∥面CA1D；
（2）解：AC=BC，D是AB的中点，AB⊥CD，
又AA1⊥面ABC，CD?面ABC，AA1⊥CD，
AA1∩AB=A，CD⊥面AA1B1B，CD?面CA1D，
平面CA1D⊥平面AA1B1B所以CD是三棱锥B1-A1DC的高，
又S△A1B1D=
AB×
=
，
所以VB1-A1DC=VC-A1B1D=
S△A1B1D×AD=
×
×
=1；
（Ⅰ）证明：连接AC1交A1C于点E，连接DE因为四边形AA1C1C是矩形，则E为AC1的中点
又D是AB的中点，DE∥BC1，
又DE?面CA1D，BC1?面CA1D，
所以BC1∥面CA1D；
（2）解：AC=BC，D是AB的中点，AB⊥CD，
又AA1⊥面ABC，CD?面ABC，AA1⊥CD，
AA1∩AB=A，CD⊥面AA1B1B，CD?面CA1D，
平面CA1D⊥平面AA1B1B所以CD是三棱锥B1-A1DC的高，
又S△A1B1D=
| 1 |
| 2 |
| 3 |
| 3 |
所以VB1-A1DC=VC-A1B1D=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评：本题考查了三棱柱中线面平行的判断以及棱锥的体积的求法，关键是转化为线线平行的判断以及棱锥的高的求法．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知sin
=m（|m|≤1），则cos（π+α）等于（ ）
| α |
| 2 |
| A、1-2m2 | ||
| B、2m2-1 | ||
C、
| ||
| D、2m-1 |