题目内容
3.设函数f(x)=sinx-cosx+x+1,0<x<2π,求函数f(x)的单调区间与极值.分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可.
解答 解:由f(x)=sinx-cosx+x+1,0<x<2π,
得f'(x)=cosx+sinx+1,
于是$f'(x)=1+\sqrt{2}sin({x+\frac{π}{4}})$.
令f'(x)=0,从而$sin({x+\frac{π}{4}})=-\frac{{\sqrt{3}}}{2}$,
得x=π或$x=\frac{3π}{2}$.
当x变化时,f'(x),f(x)的变化情况如下表:
| x | (0,π) | π | $({0,\frac{3}{2}π})$ | $\frac{3}{2}π$ | $({\frac{3}{2}π,2π})$ |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | π+2 | 单调递减 | $\frac{3}{2}π$ | 单调递增 |
故函数的极小值为$f({\frac{3π}{2}})=\frac{3π}{2}$,极大值为f(π)=π+2.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及三角函数问题,是一道中档题.

练习册系列答案
相关题目
18.已知曲线y=x3在(a,b)处的切线斜率为3,那么a的值是( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 2 |
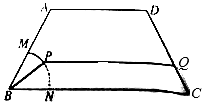 如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.
如图,某公园中间有一块等腰梯形的绿化区ABCD,AB,CD的长度相等,均为2百米,BC的长度为4百米,其中BMN是半径为1百米的扇形,$∠ABC=\frac{π}{3}$.管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$;其中P为$\widehat{MN}$上异于M,N的一点,小路PQ与BC平行,设∠PBC=θ.