Question

13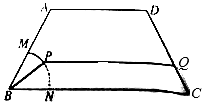．如图，某公园中间有一块等腰梯形的绿化区ABCD，AB，CD的长度相等，均为2百米，BC的长度为4百米，其中BMN是半径为1百米的扇形，$∠ABC=\frac{π}{3}$．管理部门欲在绿化区ABCD中修建从M到C的观赏小路$\widehat{MP}-PQ-QC$；其中P为$\widehat{MN}$上异于M，N的一点，小路PQ与BC平行，设∠PBC=θ．
（1）用θ表示PQ的长度，并写出θ的范围；
（2）当θ取何值时，才能使得修建的观赏小路$\widehat{MP}-PQ-QC$的总长度最短？并说明理由．

Answer 1

分析 （1）过P作PP₁⊥BC于P₁，过Q作QQ₁⊥BC于Q₁，先计算BN，PP₁，再得出CQ₁即可得出PQ的长；
（2）求出观赏小路长度关于θ的函数f（θ），利用导数求出f（θ）的单调性，总而得出观赏小路最小时对应的θ值．

解答 解：（1）过P作PP₁⊥BC于P₁，过Q作QQ₁⊥BC于Q₁，
∵∠PBC=θ，BP=1，
∴QQ₁=PP₁=sinθ，BP₁=cosθ，
在Rt△QCQ₁中，tan∠QCQ₁=$\frac{Q{Q}_{1}}{C{Q}_{1}}$=$\sqrt{3}$，∴CQ₁=$\frac{\sqrt{3}}{3}$sinθ，
∴PQ=P₁Q₁=4-cosθ-$\frac{\sqrt{3}}{3}$sinθ，（0＜θ＜$\frac{π}{3}$），
（2）在Rt△QCQ₁中，sin∠QCQ₁=$\frac{Q{Q}_{1}}{CQ}$=$\frac{\sqrt{3}}{2}$，∴CQ=$\frac{2\sqrt{3}}{3}$sinθ，
∵∠PBC=θ，∠ABC=$\frac{π}{3}$，BP=1，
∴$\widehat{MP}$=$\frac{π}{3}$-θ，
设观赏小路的总长度为f（θ），则f（θ）=$\frac{π}{3}$-θ+4-cosθ-$\frac{\sqrt{3}}{3}$sinθ+$\frac{2\sqrt{3}}{3}$sinθ=$\frac{π}{3}$-θ+4-cosθ+$\frac{\sqrt{3}}{3}$sinθ（0＜θ＜$\frac{π}{3}$），
∴f′（θ）=sinθ+$\frac{\sqrt{3}}{3}$cosθ-1=$\frac{2\sqrt{3}}{3}$sin（$θ+\frac{π}{6}$）-1，
令f′（θ）=0得sin（$θ+\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$，解得θ=$\frac{π}{6}$，
当0＜θ＜$\frac{π}{6}$时，f′（θ）＜0，当$\frac{π}{6}$＜θ＜$\frac{π}{3}$时，f′（θ）＞0，
∴f（θ）在（0，$\frac{π}{6}$）上单调递减，在（$\frac{π}{6}$，$\frac{π}{3}$）上单调递增，
∴当θ=$\frac{π}{6}$时，f（θ）取得最小值，
∴当θ=$\frac{π}{6}$时，观赏小路$\widehat{MP}-PQ-QC$的总长度最短．

点评 本题考查了函数解析式的求解，导数与函数最值的关系，属于中档题．