题目内容

函数y=x•e-x在x∈[2，4]上的最小值为（　　）
A、0
B、
1
e
C、
4
e4
D、
2
e2
考点：函数的最值及其几何意义
专题：导数的概念及应用
分析：求出导函数，x∈[2，4]时，y′＜0，y=x•e-x单调递减，从而求出函数的最值．
解答： 解：∵y=x•e-x，∴y′=（1-x）•e-x
当x∈[2，4]时，y′＜0，y=x•e-x单调递减，
∴当x=4时，y=x•e-x有最小值，且y=
4
e4
．
故选：C．
点评：本题考查的是利用导数，判断函数的单调性，从而求出最值，属于基础题．
练习册系列答案
相关题目
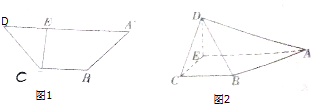如图1，在等腰梯形ABCD中，AD∥BC，AD=3BC，CD=
2
BC，过C作CE⊥AD于E，沿CE折叠，使平面DCE⊥平面ABCE，如图2．
（1）如果在AD上存在一点F，使BF∥平面DCE，证明：F为AD的中点；
（2）求二面角C-BD-A的大小．
已知向量
a
，
b
满足(
.
a
+2
b
)•(
a
-
b
)=-6，且|
a
|=1，|
b
|=2，则
a
在
b
上的投影为
 
．
投掷六个面分别记有1，2，2，3，3，3的两颗骰子
（1）求所出现的点数均为2的概率；
（2）求所出现的点数之和为4的概率．
已知向量
a
=（1，-1），
b
=（1，2），向量
c
满足（
c
+
b
）⊥
a
，（
c
-
a
）∥
b
，则
c
=
 
．
已知f（x）对任意的实数m，n都有：f（m+n）=f（m）+f（n）-1，且当x＞0时，有f（x）＞1．
（1）求f（0）；
（2）求证：f（x）在R上为增函数；
（3）若f（1）=2，且关于x的不等式f（ax-2）+f（x-x2）＜3对任意的x∈[1，+∞）恒成立，求实数a的取值范围．
设函数f（x）=
a
•
b
，其中向量
a
=（
2
cosx+1，
3
cosx），
b
=（
2
cosx-1，2sinx），x∈R．
（Ⅰ）求f（x）的解析式；
（Ⅱ）求f（x）的最小正周期、对称轴方程和对称中心的坐标．
在△ABC中，AB=3，AC=5，BC=7，且在△ABC所在的平面内存在一点O，使得（
OA
+
OB
）•
AB
=（
OB
+
OC
）•
BC
=（
OC
+
OA
）•
CA
=0成立，则
AO
•
BC
的值为（　　）
A、7B、8C、9D、10
设正四面体ABCD的所有棱长都为1米，有一只蚂蚁从点A开始按以下规则前进：在每一个顶点处等可能的选择通过这个顶点的三条棱之一，并且沿着这条棱爬到尽头，
（1）求它爬了4米之后恰好位于顶点A的概率
（2）求它爬了3米后经过B的次数x的分布列和均值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网