题目内容
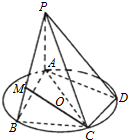如图AC是圆O的直径，B、D是圆O上两点，AC=2BC=2CD=2，PA⊥圆O所在的平面，| BM |
| 1 |
| 3 |
| BP |
（1）求证：CM∥平面PAD；
（2）若CM与平面PAC所成角的正弦值为
| ||
| 5 |
考点：直线与平面所成的角,直线与平面平行的判定
专题：空间位置关系与距离,空间角
分析：（Ⅰ）作ME⊥AB于E，连接CE，则ME∥AP，由AC是圆O的直径，得到∠BCE=∠ECA=30°=∠CAD，从而EC∥AD，由此能证明CM∥平面PAD．
（Ⅱ）以A为原点，直线AB，AP分别为x，z轴建立空间坐标系，求出面PAC的法向量为
=（x，y，z），利用向量法能求出AP的值．
（Ⅱ）以A为原点，直线AB，AP分别为x，z轴建立空间坐标系，求出面PAC的法向量为
| n |
解答：
解：（Ⅰ）证明：作ME⊥AB于E，连接CE，则ME∥AP，…①
∵AC是圆O的直径，AC=2BC=2CD=2，
∴AD⊥DC，AB⊥BC，∴∠BAC=∠CAD=30°，…（2分）
∠BCA=∠DCA=60°，AB=AD=
，
=
，∴
=
=
，tan∠BCE=
=
，
∴∠BCE=∠ECA=30°=∠CAD，∴EC∥AD，…②，…（4分）
由①②，且ME∩CE=E，
得平面MEC∥平面PAD，CM?平面MEC，CM?平面PAD，
∴CM∥平面PAD． …（6分）
（Ⅱ）解：依题意，如图以A为原点，直线AB，AP分别为x，z轴建立空间坐标系，
设AP=a，则A（0，0，0），B（
，0，0），C（
，1，0），P（0，0，a），D（
，
，0），
设面PAC的法向量为
=（x，y，z），设CM与平面PAC所成角为θ，
，
设x=
，∴
=（
，-3，0），…（8分）
=
+
=
+
，∴
=(-
，-1，
)，
∴sinθ=|cos＜
，
＞|=
=
=
=
，…（10分）
解得a=
．∴AP的值为
．…（12分）
解：（Ⅰ）证明：作ME⊥AB于E，连接CE，则ME∥AP，…①∵AC是圆O的直径，AC=2BC=2CD=2，
∴AD⊥DC，AB⊥BC，∴∠BAC=∠CAD=30°，…（2分）
∠BCA=∠DCA=60°，AB=AD=
| 3 |
| BM |
| 1 |
| 3 |
| BP |
| BE |
| 1 |
| 3 |
| BA |
| ||
| 3 |
| BE |
| BC |
| ||
| 3 |
∴∠BCE=∠ECA=30°=∠CAD，∴EC∥AD，…②，…（4分）
由①②，且ME∩CE=E，
得平面MEC∥平面PAD，CM?平面MEC，CM?平面PAD，
∴CM∥平面PAD． …（6分）
（Ⅱ）解：依题意，如图以A为原点，直线AB，AP分别为x，z轴建立空间坐标系，
设AP=a，则A（0，0，0），B（
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
设面PAC的法向量为
| n |
，
设x=
| 3 |
| n |
| 3 |
| CM |
| CB |
| BM |
| CB |
| 1 |
| 3 |
| BP |
| CM |
| ||
| 3 |
| a |
| 3 |
∴sinθ=|cos＜
| CM |
| n |
|
| ||||
|
|
=
| 2 | ||||||
|
| ||
|
| ||
| 5 |
解得a=
| 3 |
| 3 |
点评：本题考查直线与平面垂直的判定定理、平面与平面垂直的性质定理、勾股定理、二面角的求解等基础知识和空间向量的立体几何中的应用，意在考查方程思想、等价转化思想等数学思想方法和考生的空间想象能力、逻辑推理能力和运算求解能力．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，动物园要建造2间面积相同的矩形动物居室，如果可供建造围墙的材料总长是24m，设这两间动物居室的宽为x（单位：m），两间动物居室总面积为y（单位：m2），（注：围墙的厚度忽略不计）设函数f（x）=2cos2x+
sin2x，x∈R，则下列结论正确的是（ ）
| 3 |
A、f（x）的图象关于直线x=
| ||
| B、f（x）的最大值是2 | ||
C、f（x）在[0，
| ||
D、f（x）的图象关于点（
|
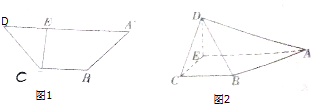如图1，在等腰梯形ABCD中，AD∥BC，AD=3BC，CD=
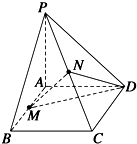如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，M，N分别是AB、PC的中点