题目内容
(1)函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值与最小值之和为6,求a的值;
(2)0≤x≤2,求函数y=4 x-
-3•2x+5的最大值和最小值.
(2)0≤x≤2,求函数y=4 x-
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)根据指数函数的性质建立方程关系即可求a的值;
(2)利用换元法设t=2x,将函数转化为关于t的一元二次函数,利用一元二次函数的性质即可得到结论.
(2)利用换元法设t=2x,将函数转化为关于t的一元二次函数,利用一元二次函数的性质即可得到结论.
解答:
解:(1)函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值与最小值之和为6,
则a+a2=6,
即a2-a-6=0,
解得a=3或a=-2(舍),
故a=3;
(2)y=4 x-
-3•2x+5=
•4x-3•2x+5=
•(2x)2-3•2x+5,
设t=2x,∵0≤x≤2,∴1≤t≤4,
则函数等价为y=g(t)=
•t2-3•t+5=
•(t-3)2+
,
∴当t=3时,函数取得最小值为g(3)=
,
当t=1时,函数取得最大值为g(1)=
.
则a+a2=6,
即a2-a-6=0,
解得a=3或a=-2(舍),
故a=3;
(2)y=4 x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设t=2x,∵0≤x≤2,∴1≤t≤4,
则函数等价为y=g(t)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当t=3时,函数取得最小值为g(3)=
| 1 |
| 2 |
当t=1时,函数取得最大值为g(1)=
| 5 |
| 2 |
点评:本题主要考查函数最值的应用,利用指数函数单调性和一元二次函数的性质是解决本题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图所示,动物园要建造2间面积相同的矩形动物居室,如果可供建造围墙的材料总长是24m,设这两间动物居室的宽为x(单位:m),两间动物居室总面积为y(单位:m2),(注:围墙的厚度忽略不计)
如图所示,动物园要建造2间面积相同的矩形动物居室,如果可供建造围墙的材料总长是24m,设这两间动物居室的宽为x(单位:m),两间动物居室总面积为y(单位:m2),(注:围墙的厚度忽略不计)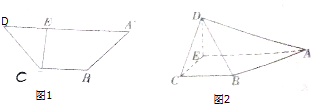 如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=
如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=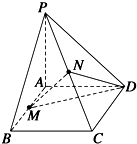 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB、PC的中点
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB、PC的中点