题目内容
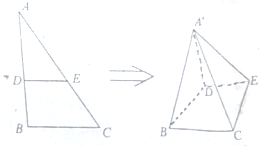如图，在直角△ABC中，B=90°，BC=1，AB=| 3 |
| AD |
| AB |
| AE |
| AC |
（Ⅰ）证明：DE⊥A′B；
（Ⅱ）是否存在这样的实数λ，使得二面角B-A′C-E的大小为90°，如果存在，请求出λ的值；若不存在，请说明理由．
考点：二面角的平面角及求法,直线与平面垂直的性质
专题：空间位置关系与距离,空间角
分析：（Ⅰ）由已知得DE⊥AB，从而折叠后DE⊥A′D，DE⊥BD．由此能证明DE⊥A′B．
（Ⅱ）以D点为原点，DE为x轴，DB为y轴，DA'为z轴，建立空间直角坐标系，分别求出面A′BC的法向量和面A′EC的法向量，由二面角B-A′C-E的大小为90°，能坟出存在λ=
满足条件．
（Ⅱ）以D点为原点，DE为x轴，DB为y轴，DA'为z轴，建立空间直角坐标系，分别求出面A′BC的法向量和面A′EC的法向量，由二面角B-A′C-E的大小为90°，能坟出存在λ=
| 1 |
| 2 |
解答：
（Ⅰ）证明：∵在直角△ABC中，B=90°，BC=1，AB=
，
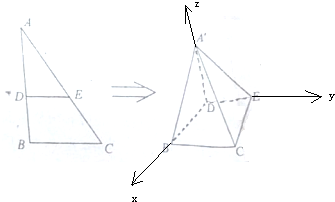
其中D，E分别是线段AB和AC的点，
且
=
=λ（0＜λ＜1），
∴DE⊥AB，∴折叠后DE⊥A′D，DE⊥BD．
又A′D∩BD=D，∴DE⊥平面A′DB，
又A′B?平面A′DB，∴DE⊥A′B．
（Ⅱ）解：以D点为原点，DE为x轴，DB为y轴，
DA'为z轴，建立空间直角坐标系，
A′（0，0，
λ），E（λ，0，0），
B（0，
（1-λ），0），C（1，
（1-λ），0），
=（0，
λ-
，
λ），
=（1，0，0），
设面A′BC的法向量为
=（x，y，z），
则
，取y=1，得
=（0，1，
-1），
=（-λ，0，
λ），
=（1-λ，
(1-λ)，0），
设面A′EC的法向量为
=（a，b，c），
则
，取a=
，得
=（
，-1，1），
∵二面角B-A′C-E的大小为90°，
∴
•
=
×0-1×1+
-1=0，
解得λ=
，故存在λ=
满足条件．
| 3 |
其中D，E分别是线段AB和AC的点，
且
| AD |
| AB |
| AE |
| AC |
∴DE⊥AB，∴折叠后DE⊥A′D，DE⊥BD．
又A′D∩BD=D，∴DE⊥平面A′DB，
又A′B?平面A′DB，∴DE⊥A′B．
（Ⅱ）解：以D点为原点，DE为x轴，DB为y轴，
DA'为z轴，建立空间直角坐标系，
A′（0，0，
| 3 |
B（0，
| 3 |
| 3 |
| BA′ |
| 3 |
| 3 |
| 3 |
| BC |
设面A′BC的法向量为
| n |
则
|
| n |
| 1 |
| λ |
| EA′ |
| 3 |
| EC |
| 3 |
设面A′EC的法向量为
| m |
则
|
| 3 |
| m |
| 3 |
∵二面角B-A′C-E的大小为90°，
∴
| n |
| m |
| 3 |
| 1 |
| λ |
解得λ=
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题主要考查直线与平面之间的平行、垂直等位置关系，线线垂直、二面角的概念、求法等知识，以及空间想象能力和逻辑推理能力．
练习册系列答案
名校课堂系列答案
相关题目
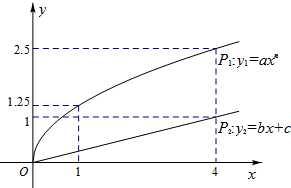某企业拟用10万元投资甲、乙两种商品．已知各投入x万元，甲、乙两种商品可分别获得y1，y2万元的利润，利润曲线P1，P2如图所示．问怎样分配投资额，才能使投资获得最大利润？
如图所示，动物园要建造2间面积相同的矩形动物居室，如果可供建造围墙的材料总长是24m，设这两间动物居室的宽为x（单位：m），两间动物居室总面积为y（单位：m2），（注：围墙的厚度忽略不计）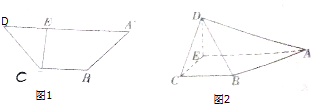
如图1，在等腰梯形ABCD中，AD∥BC，AD=3BC，CD=