题目内容
求y=x+
的值域.
| 1-x |
考点:函数的值域
专题:函数的性质及应用
分析:令
=t(t≥0)换元,转化为关于t的二次函数求得函数的值域.
| 1-x |
解答:
解:令
=t(t≥0),
则1-x=t2,x=1-t2,
∴y=x+
=1-t2+t=-t2+t+1(t≥0),
当t=
时y有最大值,等于
.
∴y=x+
的值域是(-∞,
].
| 1-x |
则1-x=t2,x=1-t2,
∴y=x+
| 1-x |
当t=
| 1 |
| 2 |
| 5 |
| 4 |
∴y=x+
| 1-x |
| 5 |
| 4 |
点评:本题考查了利用换元法求函数的值域,训练了二次函数值域的求法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个圆锥的表面积为π,它的侧面展开图是圆心角为120°的扇形,则该圆锥的高为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
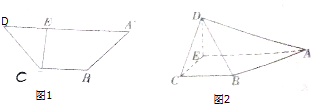 如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=
如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=