题目内容
设函数f(log2x)=
(1)求f(x)的解析式;
(2)若f(2x2-λx)≥
对任意x∈[
,1]恒成立,求常数λ的取值范围.
| x |
| x2+1 |
(1)求f(x)的解析式;
(2)若f(2x2-λx)≥
| 2 |
| 5 |
| 1 |
| 2 |
考点:函数解析式的求解及常用方法,函数恒成立问题
专题:函数的性质及应用
分析:(1)换元,令t=log2x,则x=2t,故f(t)=
,故f(x)=
;
(2)先验证函数为偶函数,再由f(2x2-λx)≥
=f(1)?f(|2x2-λx|)≥f(1),进一步λ≤2x-
的最小值,或λ≥2x+
的最大值,
求最值即可解决.
| 2t |
| 22t+1 |
| 2x |
| 22x+1 |
(2)先验证函数为偶函数,再由f(2x2-λx)≥
| 2 |
| 5 |
| 1 |
| x |
| 1 |
| x |
求最值即可解决.
解答:
解:(1)令t=log2x,则x=2t,故f(t)=
,故f(x)=
;
(2)f(-x)=
=
=
=f(x),故函数f(x)为偶函数且在[0,+∞)递增,
又f(1)=
,∴f(2x2-λx)≥
=f(1)?f(|2x2-λx|)≥f(1),
∴|2x2-λx|≥1,
∴2x2-λx≥1,或2x2-λx≤-1,
∴2x2-1≥λx,或2x2+1≤λx,
∴λ≤2x-
,或λ≥2x+
,
∴λ≤2x-
的最小值,或λ≥2x+
的最大值,
∵x∈[
,1]时2x-
的最小值为-1,2x+
的最大值为3,
∴λ≤-1或λ≥3,
故λ的取值范围为{λ|λ≤-1或λ≥3}.
| 2t |
| 22t+1 |
| 2x |
| 22x+1 |
(2)f(-x)=
| 2-x |
| 2-2x+1 |
| 2-x•22x |
| 2-2x•22x+22x |
| 2x |
| 22x+1 |
又f(1)=
| 2 |
| 5 |
| 2 |
| 5 |
∴|2x2-λx|≥1,
∴2x2-λx≥1,或2x2-λx≤-1,
∴2x2-1≥λx,或2x2+1≤λx,
∴λ≤2x-
| 1 |
| x |
| 1 |
| x |
∴λ≤2x-
| 1 |
| x |
| 1 |
| x |
∵x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| x |
∴λ≤-1或λ≥3,
故λ的取值范围为{λ|λ≤-1或λ≥3}.
点评:本题主要考查函数解析式的求法,同时考查函数与不等式的关系,做题时要注意转化.

练习册系列答案
相关题目
已知正方形ABCD的边长为2,P是平面ABCD外一点,且PA=PB=PC=PD=2
,则PA与平面ABCD所成的角是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
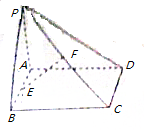 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.