题目内容

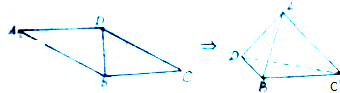
已知正方形ABCD的边长为2，P是平面ABCD外一点，且PA=PB=PC=PD=2
2
，则PA与平面ABCD所成的角是（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
考点：直线与平面所成的角
专题：空间角
分析：由题意，P在平面ABCD中的射影为正方形ABCD的中心，求出正方形ABCD的对角线长，利用余弦函数，即可求出PA与平面ABCD所成的角．
解答： 解：设PA与平面ABCD所成的角是α．
由题意，P在平面ABCD中的射影为正方形ABCD的中心，
∵正方形ABCD的边长为2，
∴正方形ABCD的对角线长为2
2
，
∵PA=2
2
，
∴cosα=
2
2
2
=
1
2
，
∴α=
π
3
．
∴PA与平面ABCD所成的角是
π
3
．
故选：C．
点评：本题考查线面平行，线面垂直的性质的应用，考查线面所成角的求法，解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用，是中档题．
练习册系列答案
相关题目
已知ABCD中，AD=BC．AD∥BC，且AB=3
2
，AD=2
3
．BD=
6
，沿BD将其折成一个二面角A-BD-C，使得AB⊥CD．
（1）求二面角A-BD-C的大小；
（2）求折后点A到面BCD的距离．
已知函数f（x）=4sinxcos（x+
π
3
）+
3
．
（1）f（x）在区间[-
π
4
，
π
6
]上的最大值和最小值及取得最值时x的值．
（2）若方程f（x）-t=0在x∈[-
π
4
，
π
2
]上有唯一解，求实数t的取值范围．
已知函数f（x）=
1
2
sin2x•sinφ+cos2x•cosφ+
1
2
sin（
3
2
π-φ）（0＜φ＜π），其图象过点（
π
6
，
1
2
．）
（Ⅰ）求函数f（x）在[0，π]上的单调递减区间；
（Ⅱ）若x0∈（
π
2
，π），sinx0=
3
5
，求f（x0）的值．
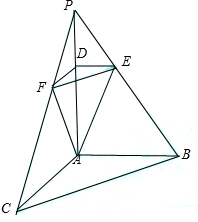在三棱椎P-ABC中，PA⊥平面ABC，AC=AB=
3
，BC=
6
，∠PBA=
π
3
，点D，E，F分别是PA、PB、PC上的点并且满足PD：PA=PE：PB=PF：PC=1：3
（Ⅰ）求证：AB⊥DF；
（Ⅱ）设平面ABC与平面AEF所成角为θ，求cosθ的值．
设空间任意一点O和不共线三点A、B、C，若点P满足向量关系
OP
=x
OA
-
OB
+3
OC
，且P、A、B、C四点共面，则x=
 
．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F（1，0），过点F且与坐标轴不垂直的直线与椭圆交于 P，Q两点，当直线 PQ经过椭圆的一个顶点时其倾斜角恰好为60°．
（1）求椭圆C的方程；
（2）设O为坐标原点，线段OF上是否存在点T（t，0），使得
QP
•
TP
=
PQ
•
TQ
？若存在，求出实数t的取值范围；若不存在，说明理由．
设函数f（log2x）=
x
x2+1

（1）求f（x）的解析式；
（2）若f（2x2-λx）≥
2
5
对任意x∈[
1
2
，1]恒成立，求常数λ的取值范围．
已知定点A（-2，0），F（1，0），定直线l：x=4，动点P与点F的距离是它到直线l的距离的
1
2
．设点P的轨迹为C，过点F的直线交C于D、E两点，直线AD、AE与直线l分别相交于M、N两点．
（1）求C的方程；
（2）试判断以线段MN为直径的圆是否过点F，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网