题目内容
用归纳法证明:?n∈N*,3n>n2-
.
| 3 |
| 2 |
考点:数学归纳法
专题:归纳法,推理和证明
分析:先验证n=1,2,3时的情况,再假设n=k时,原不等式也成立,由此推出n=k+1≥4时,原不等式也成立,根据归纳法原理可知,对?n∈N*,原不等式成立.
解答:
证明:(1)n=1时,31>12-
,
n=2时,32>22-
,
n=3时,33>32-
.
(2)假设n=k时,原不等式也成立,即3k>k2-
,
则当n=k+1时,有3k+1=3•3k>3(k2-
).
由3(k2-
)-[(k+1)2-
]=2k2-2k-4=2(k-2)(k+1)知,
当k≥3时,2(k-2)(k+1)>0,∴3(k2-
)>(k+1)2-
,
∴3k+1>(k+1)2-
.
即n=k+1≥4时,原不等式成立,
综合(1)、(2)知,对?n∈N*,3n>n2-
.
| 3 |
| 2 |
n=2时,32>22-
| 3 |
| 2 |
n=3时,33>32-
| 3 |
| 2 |
(2)假设n=k时,原不等式也成立,即3k>k2-
| 3 |
| 2 |
则当n=k+1时,有3k+1=3•3k>3(k2-
| 3 |
| 2 |
由3(k2-
| 3 |
| 2 |
| 3 |
| 2 |
当k≥3时,2(k-2)(k+1)>0,∴3(k2-
| 3 |
| 2 |
| 3 |
| 2 |
∴3k+1>(k+1)2-
| 3 |
| 2 |
即n=k+1≥4时,原不等式成立,
综合(1)、(2)知,对?n∈N*,3n>n2-
| 3 |
| 2 |
点评:本题考查了利用数学归纳法证明不等式,值得注意的是,至少应验证n的前3个值,因为在第(2)部分中,当k≥3时,对不等式放缩才有效.

练习册系列答案
相关题目
设集合A={(x,y)|y=x}与集合B={(x,y)|x=a+
,a∈R},若A∩B的元素只有一个,则实数a的取值范围是( )
| 1-y2 |
A、a=±
| ||
B、-1<a<1或a=±
| ||
C、a=
| ||
D、-1<a≤1或a=-
|
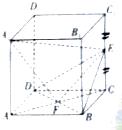 如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点.
如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点.