题目内容
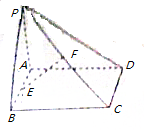 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若PA=AD,求一面直线EF与BC所成的夹角.
考点:直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)取PD中点Q,连AQ、QF,则AE∥QF,四边形AEFQ为平行四边形,由此能证明EF∥面PAD.
(2)由CD⊥AD,CD⊥PA,得CD⊥面PAD,由EF∥AQ,得EF⊥CD.
(3)由已知得△PAD为等腰直角三角形AQ⊥PD,∠QAD=45°,由此能求出EF与BC所成角为45°.
(2)由CD⊥AD,CD⊥PA,得CD⊥面PAD,由EF∥AQ,得EF⊥CD.
(3)由已知得△PAD为等腰直角三角形AQ⊥PD,∠QAD=45°,由此能求出EF与BC所成角为45°.
解答:
(1)证明:取PD中点Q,连AQ、QF,则AE∥QF,
∴四边形AEFQ为平行四边形,∴EF∥AQ,
又∵AQ?平面PAD,EF?平面PAD,
∴EF∥面PAD.
(2)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,
PA?平面PAD,AD?平面PAD,
∴CD⊥面PAD,又∵AQ?平面PAD,∴CD⊥AQ
∵EF∥AQ,∴EF⊥CD.
(3)解:∵PA=AD,PA⊥平面ABCD,∠PDA=45°
∴△PAD为等腰直角三角形
∴AQ⊥PD,
∴∠QAD=45°
又∵AQ∥EF,AD∥BC,
∴EF与BC所成角为45°.

∴四边形AEFQ为平行四边形,∴EF∥AQ,
又∵AQ?平面PAD,EF?平面PAD,
∴EF∥面PAD.
(2)证明:∵CD⊥AD,CD⊥PA,PA∩AD=A,
PA?平面PAD,AD?平面PAD,
∴CD⊥面PAD,又∵AQ?平面PAD,∴CD⊥AQ
∵EF∥AQ,∴EF⊥CD.
(3)解:∵PA=AD,PA⊥平面ABCD,∠PDA=45°
∴△PAD为等腰直角三角形
∴AQ⊥PD,
∴∠QAD=45°
又∵AQ∥EF,AD∥BC,
∴EF与BC所成角为45°.
点评:本题考查线面平行,线面垂直的证明,考查直线与平面所成角的求法,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用,是中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知f(x)=
sinxcosx-cos2x+
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c-
a,则f(B)的取值范围( )
| 3 |
| 1 |
| 2 |
| 3 |
A、(-1,
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
若A、B两点的坐标分别是A(3cosa,3sina,1),B(2cosb,2sinb,1),则|
|的取值范围是( )
| AB |
| A、[0,5] |
| B、[1,5] |
| C、(1,5) |
| D、[1,25] |
已知数列{an}满足a1=1,an+1=an+n+2n(n∈N*),则an等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
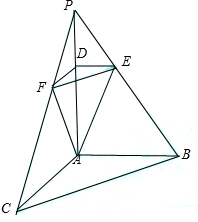 在三棱椎P-ABC中,PA⊥平面ABC,AC=AB=
在三棱椎P-ABC中,PA⊥平面ABC,AC=AB=