题目内容
直线x=0，x=2，y=0与曲线y=x2+1围成的曲边梯形，将区间[0，2]5等分，按照区间左端点和右端点估计梯形面积分别为 、 ．
考点：定积分在求面积中的应用
专题：导数的综合应用
分析：根据区间左端点和右端点对应的小曲边梯形近似为小矩形，由此利用5个小矩形的面积代替曲边梯形的面积．
解答：
解：将区间[0，2]5等分，每个区间长度为0.4，按照区间左端点和右端点对应的小曲边梯形的面积近似为小矩形的面积，
所以按照区间左端点和右端点估计梯形面积分别为0.4×（0.42+1）×5和0.4×（22+1）×5，即为2.32和10．
故答案为2.32；10．
所以按照区间左端点和右端点估计梯形面积分别为0.4×（0.42+1）×5和0.4×（22+1）×5，即为2.32和10．
故答案为2.32；10．
点评：本题考查了曲边梯形面积的求法，利用了分割和近似求值．
练习册系列答案
相关题目
已知数列{an}满足a1=1，an+1=an+n+2n（n∈N*），则an等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
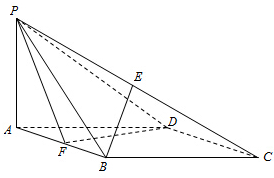如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，AB=2，PA=1，PA⊥平面ABCD，E是PC的中点，F是AB的中点．