题目内容
15.△ABC满足下列条件:①b=12,c=9,C=60°②b=3,c=4,B=30°;③b=3$\sqrt{3}$,c=6,B=60°;④a=5,b=8,A=30°.其中有两个解的是( )| A. | ①② | B. | ②③ | C. | ①③④ | D. | ②④ |
分析 △ABC中,当A为锐角时,a<bsin A,无解.当A为钝角或直角时,a≤b,无解,当bsinA<a<b时,三角形有两个解,利用正弦定理,正弦函数的图象和性质逐一判断即可得解.
解答 解:①b=12,c=9,C=60°;
由正弦定理可得:sinB=$\frac{12×\frac{\sqrt{3}}{2}}{9}=\frac{2\sqrt{3}}{3}$>1,三角形无解,不符合条件;
②b=3,c=4,B=30°;
有:csinB=4×$\frac{1}{2}$=2<b<c,三角形有两解,符合条件;
③b=3$\sqrt{3}$,c=6,B=60°;
由正弦定理可得:sinC=$\frac{6×\frac{\sqrt{3}}{2}}{3\sqrt{3}}$=1,C为直角,由c<b,可得三角形无解,不符合条件;
④a=5,b=8,A=30°.
可得:bsinA=4<a<b,三角形有两解,符合条件;
故选:D.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
3.已知x>-2,则x+$\frac{1}{x+2}$的最小值为( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | 2 | D. | 0 |
10.已知p:(x-2)(x+1)>0;q:|x|<a,若¬p是q的必要不充分条件,则a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
4.在△ABC中,若A=60°,b=4,此三角形面积S=2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
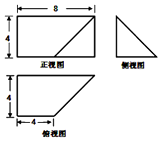 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.