题目内容
20.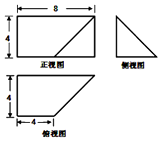 一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
一个几何体的三视图如图所示(单位:cm),则该几何体的表面积为64+32$\sqrt{2}$cm2,体积为$\frac{160}{3}$cm.
分析 由题意,直观图为三棱柱,割去一个三棱锥,三棱柱的底面是直角边为4cm的等腰直角三角形,高为8cm,三棱锥的底面是直角边为4cm的等腰直角三角形,高为4cm,即可求出几何体的表面积、体积.
解答 解:由题意,直观图为三棱柱,割去一个三棱锥,三棱柱的底面是直角边为4cm的等腰直角三角形,高为8cm,三棱锥的底面是直角边为4cm的等腰直角三角形,高为4cm,
几何体的表面积为$\frac{1}{2}×4×4+\frac{1}{2}×4×4\sqrt{2}+\frac{1}{2}×4×8+\frac{4+8}{2}×4\sqrt{2}$+$\frac{4+8}{2}×4$=64+32$\sqrt{2}$cm2,
体积为$\frac{1}{2}×4×4×8-\frac{1}{3}×\frac{1}{2}×4×4×4$=$\frac{160}{3}$cm3.
故答案为64+32$\sqrt{2}$,$\frac{160}{3}$.
点评 本题考查由三视图求面积、体积、考查学生的计算能力,确定直观图的现状是关键.

练习册系列答案
相关题目
8.若a=20.5,b=log0.25,c=0.52,则a、b、c三个数的大小关系式( )
| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | b<a<c |
9.已知sinα=$\frac{4}{5}$,α∈($\frac{π}{2}$,π),则sin2α的值为( )
| A. | $\frac{7}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{24}{25}$ | D. | -$\frac{12}{25}$ |
8.以圆C1:x2+y2+4x+1=0与圆C2:x2+y2+2x+2y+1=0相交的公共弦为直径的圆的方程为( )
| A. | (x-1)2+(y-1)2=1 | B. | (x+1)2+(y+1)2=1 | C. | (x+$\frac{3}{5}$)2+(y+$\frac{6}{5}$)2=$\frac{4}{5}$ | D. | (x-$\frac{3}{5}$)2+(y-$\frac{6}{5}$)2=$\frac{4}{5}$ |
15.△ABC满足下列条件:①b=12,c=9,C=60°②b=3,c=4,B=30°;③b=3$\sqrt{3}$,c=6,B=60°;④a=5,b=8,A=30°.其中有两个解的是( )
| A. | ①② | B. | ②③ | C. | ①③④ | D. | ②④ |
10.函数$f(x)={2}^{x}+\frac{1}{4•{2}^{x}}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |