题目内容
7.已知点P是抛物线y2=4x上一点,设点P到此抛物线准线的距离是d1,到直线x+2y-12=0的距离为d2,则d1+d2的最小值是$\frac{11\sqrt{5}}{5}$.分析 直接把P到准线的距离转化为P到抛物线焦点的距离,求焦点到直线x+2y-12=0的距离得答案.
解答 解:∵点P到抛物线y2=4x的准线的距离为d1等于P到抛物线y2=4x的焦点的距离|PF|,
则d1+d2的最小值即为F到直线x+2y-12=0的距离.
由抛物线y2=4x得F(1,0),
∴d1+d2的最小值是$\frac{|1×1+2×0-12|}{\sqrt{1+4}}$=$\frac{11\sqrt{5}}{5}$.
故答案为$\frac{11\sqrt{5}}{5}$.
点评 本题考查了抛物线的简单几何性质,考查了数学转化思想方法,是基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.△ABC满足下列条件:①b=12,c=9,C=60°②b=3,c=4,B=30°;③b=3$\sqrt{3}$,c=6,B=60°;④a=5,b=8,A=30°.其中有两个解的是( )
| A. | ①② | B. | ②③ | C. | ①③④ | D. | ②④ |
19.若a=log${\;}_{\frac{1}{2}}}$3,b=log3$\frac{1}{2}$,c=20.3,则( )
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | a<c<b |
16.若不等式|x-2|+|x+3|>a恒成立,则a的取值范围是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,5) | D. | (5,+∞) |
17.已知集合M={x|x2-2x<0},N={x|x-1>0},则M∩N=( )
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x>2} | D. | {x|x<0} |
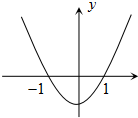 设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.
设f(x)=ax3+bx2+cx的极小值为-2,其导函数y=f′(x)的图象是经过点(-1,0),(1,0)开口向上的抛物线,如图所示.