题目内容
 如图,已知椭圆E:
如图,已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)求证:点M在直线l上;
(Ⅲ)是否存在实数k,使得四边形AOBC为平行四边形?若存在求出k的值,若不存在说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆的离心率结合焦点坐标求得a,b,则椭圆方程可求;
(Ⅱ)设出直线AB的方程,和椭圆方程联立后由根与系数的关系求得A,B两点的横坐标的和与积,由中点坐标公式得到M的横坐标,代入直线方程求得M的纵坐标,然后代入直线l的方程验证得答案;
(Ⅲ)假设存在这样的平行四边形,则M为OC中点,联立直线l的方程和椭圆方程求得C的坐标,由中点坐标公式得到M的坐标,由坐标相等求得k的值.
(Ⅱ)设出直线AB的方程,和椭圆方程联立后由根与系数的关系求得A,B两点的横坐标的和与积,由中点坐标公式得到M的横坐标,代入直线方程求得M的纵坐标,然后代入直线l的方程验证得答案;
(Ⅲ)假设存在这样的平行四边形,则M为OC中点,联立直线l的方程和椭圆方程求得C的坐标,由中点坐标公式得到M的坐标,由坐标相等求得k的值.
解答:
(Ⅰ)解:由题意可知e=
=
,c=
,于是a=2,
∴b2=a2-c2=22-(
)2=1.
∴椭圆的标准方程为
+y2=1;
(Ⅱ)证明:设A(x1,y1),B(x2,y1),M(x0,y0),
由
,即(4k2+1)x2+8
k2x+12k2-4=0.
x1+x2=
,x0=
=
,y0=k(x0+
)=
,
于是M(
,
).
∵
+4k•
=0,
∴M在直线l上;
(Ⅲ)设存在这样的平行四边形,则M为OC中点,
设点C的坐标为(x3,y3),则y0=
.
∵
,解得y3=±
.
于是
=
,解得k2=
,即k=±
.
∴当k=±
时四边形AOBC的对角线互相平分,即当k=±
时四边形AOBC是平行四边形.
| c |
| a |
| ||
| 2 |
| 3 |
∴b2=a2-c2=22-(
| 3 |
∴椭圆的标准方程为
| x2 |
| 4 |
(Ⅱ)证明:设A(x1,y1),B(x2,y1),M(x0,y0),
由
|
| 3 |
x1+x2=
-8
| ||
| 4k2+1 |
| x1+x2 |
| 2 |
-4
| ||
| 4k2+1 |
| 3 |
| ||
| 4k2+1 |
于是M(
-4
| ||
| 4k2+1 |
| ||
| 4k2+1 |
∵
-4
| ||
| 4k2+1 |
| ||
| 4k2+1 |
∴M在直线l上;
(Ⅲ)设存在这样的平行四边形,则M为OC中点,
设点C的坐标为(x3,y3),则y0=
| y3 |
| 2 |
∵
|
| 1 | ||
|
于是
| 1 | ||
2
|
| ||
| 4k2+1 |
| 1 |
| 8 |
| ||
| 4 |
∴当k=±
| ||
| 4 |
| ||
| 4 |
点评:本题主要考查椭圆方程的求法,考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系求解是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是高考试卷中的压轴题.

练习册系列答案
相关题目
已知i是虚数单位,复数z=
,则z的共轭复数
等于( )
| 4+3i |
| 1+2i |
. |
| z |
| A、-2+i | B、-2-i |
| C、2+i | D、2-i |
已知二次函数f(x)=ax2+bx+c(a>0),满足a+b+c<0,则方程f(x)=0的两根x1,x2一定满足( )
| A、x1<1且x2<1 |
| B、x1>1且x2>1 |
| C、x1,x2中一个大于1,另一个小于1 |
| D、x1+x2<1 |
“m>n>1”是“logm2<logn2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
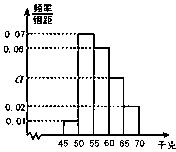 为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=
为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=