题目内容
“m＞n＞1”是“logm2＜logn2”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据对数函数的性质，利用充分条件和必要条件的定义进行判断即可．
解答：
解：不等式logm2＜logn2等价为
＜
，
若m＞n＞1，则log2m＞log2n＞0，
∴
＜
成立，即logm2＜logn2成立．
当0＜m＜1时，logm2＜0，当n＞1时，logn2＞0，满足“logm2＜logn2”，但m＞n＞1不成立，
即“m＞n＞1”是“logm2＜logn2”的充分不必要条件．
故选：A．
| 1 |
| log2m |
| 1 |
| log2n |
若m＞n＞1，则log2m＞log2n＞0，
∴
| 1 |
| log2m |
| 1 |
| log2n |
当0＜m＜1时，logm2＜0，当n＞1时，logn2＞0，满足“logm2＜logn2”，但m＞n＞1不成立，
即“m＞n＞1”是“logm2＜logn2”的充分不必要条件．
故选：A．
点评：本题主要考查充分条件和必要条件的判断，利用对数函数的性质以及不等式的性质是解决本题的关键．
练习册系列答案
相关题目
已知函数y=f（x），数列{an}的通项公式是an=f（n），n∈N*，那么“函数y=f（x）在[1，+∞﹚上单调递增”是“数列{an}是递增数列”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知复数z=
（i为虚数单位），则复数z在复平面内对应的点位于（ ）
| 2i+1 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
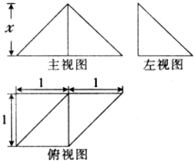如图所示是一个几何体的三视图，若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
如图，已知椭圆E：
如图，有一条光线沿直线y=4射到抛物线y2=4x上的一点P，经抛物线反射后，反射光线与抛物线的交于另一点Q，O是抛物线的顶点，F是抛物线的焦点，求弦PQ的斜率和△OPQ的面积．