题目内容
已知x>0,f(x)=
,求函数f(x)的值域.
| 2x |
| x2+1 |
考点:基本不等式在最值问题中的应用,函数的值域
专题:函数的性质及应用
分析:由x>0,得f(x)=
,求出x+
的取值范围,即得
的取值范围,求得f(x)的值域.
| 2 | ||
x+
|
| 1 |
| x |
| 2 | ||
x+
|
解答:
解:∵x>0,∴f(x)=
=
;
又∵x+
≥2
=2,
当且仅当x=1时,“=”成立,
∴0<
≤
,
∴0<
≤1;
∴函数f(x)的值域是(0,1].
| 2x |
| x2+1 |
| 2 | ||
x+
|
又∵x+
| 1 |
| x |
x•
|
当且仅当x=1时,“=”成立,
∴0<
| 1 | ||
x+
|
| 1 |
| 2 |
∴0<
| 2 | ||
x+
|
∴函数f(x)的值域是(0,1].
点评:本题考查了利用基本不等式求函数的最值,从而求出函数值域的问题,是基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知复数z=
(i为虚数单位),则复数z在复平面内对应的点位于( )
| 2i+1 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,已知椭圆E:
如图,已知椭圆E: 如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.
如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.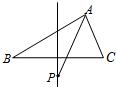 如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则
如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则