题目内容
在线段AB上任取一点P，以P为顶点，B为焦点作抛物线，则该抛物线的准线与线段AB有交点的概率是 ．
考点：几何概型
专题：概率与统计
分析：设线段AB中点C，以P为顶点，B为焦点作抛物线，如图所示，利用抛物线的对称性，得点P落在线段CB上时，满足抛物线的准线与线段AB有交点．由此结合几何概型计算公式即可算出事件的概率．
解答：
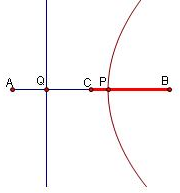解：设线段AB中点C，以P为顶点，B为焦点作抛物线，如图所示．
根据抛物线的对称性，则点P落在线段CB上时，满足抛物线的准线与线段AB有交点．
因此，事件“抛物线的准线与线段AB有交点”的概率为：P=
=
．
故答案为：
．
解：设线段AB中点C，以P为顶点，B为焦点作抛物线，如图所示．根据抛物线的对称性，则点P落在线段CB上时，满足抛物线的准线与线段AB有交点．
因此，事件“抛物线的准线与线段AB有交点”的概率为：P=
| BC |
| AB |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题给出线段AB，求线段上点P，以P为顶点，B为焦点作抛物线，则该抛物线的准线与线段AB有交点的概率，着重考查了几何概型及其计算公式的知识，属于基础题．
练习册系列答案
相关题目
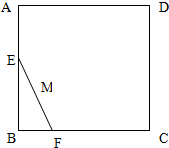如图，线段EF的长度为1，端点E、F在边长不小于1的正方形ABCD的四边上滑动，当E、F沿着正方形的四边滑动一周时，EF的中点M所形成的轨迹为G，若G的周长为L，其围成的面积为S，则L-S的最大值为（ ）| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
下列各式错误的是（ ）
| A、tan138°＜tan143° | ||||
B、sin（-
| ||||
| C、lg1.6＞lg1.4 | ||||
| D、0.75-0.1＜0.750.1 |
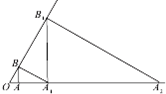如图，在△OAB中，OA⊥AB，OB=1，OA=