题目内容
10.二元线性方程组$\left\{\begin{array}{l}{x+5y=0}\\{2x+3y=4}\end{array}\right.$的系数矩阵D=( )| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
分析 利用二元线性方程组的系数矩阵的定义直接求解.
解答 解:二元线性方程组$\left\{\begin{array}{l}{x+5y=0}\\{2x+3y=4}\end{array}\right.$的系数矩阵:
D=$(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$.
故选:C.
点评 本题考查二元线性方程组的系数矩阵的求法,是基础题,解题时要认真审题,注意系数矩阵的定义的合理运用.

练习册系列答案
相关题目
20.已知集合M={x|x2+x-2<0},N={x|x+1<0},则M∩N=( )
| A. | (-1,1) | B. | (-2,-1) | C. | (-2,1) | D. | (1,2) |
1.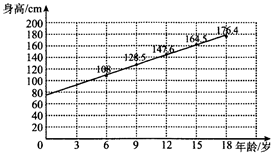 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
 某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )
某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线L.根据图中数据,下列对该样本描述错误的是( )| A. | 据样本数据估计,该地区青少年身高与年龄成正相关 | |
| B. | 所抽取数据中,5000名青少年平均身高约为145cm | |
| C. | 直线L的斜率的值近似等于样本中青少年平均身高每年的增量 | |
| D. | 从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线L上 |
10.函数y=1+3x-x3有( )
| A. | 极小值-1,极大值1 | B. | 极小值-1,极大值3 | ||
| C. | 极小值-2,极大值2 | D. | 极小值2,极大值3 |
7.为了解某公司员工的年收入和年支出的关系,随机调查了5名员工,得到如下统计数据表:
根据上表可得回归本线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.65$,$\hat a=\overline y-\hat bx$,据此估计,该公司一名员工年收入为15万元时支出为( )
| 收入x(万元) | 8.0 | 8.6 | 10.0 | 11.4 | 12.0 |
| 支出y(万元) | 4.1 | 5.2 | 6.1 | 6.7 | 7.9 |
| A. | 9.05万元 | B. | 9.25万元 | C. | 9.75万元 | D. | 10.25万元 |
8.已知菱形ABCD中,∠DAB=60°,AB=3,对角线AC与BD的交点为O,把菱形ABCD沿对角线BD折起,使得∠AOC=90°,则折得的几何体的外接球的表面积为( )
| A. | 15π | B. | $\frac{15π}{2}$ | C. | $\frac{7π}{2}$ | D. | 7π |