题目内容
3.用一根长为12的钢筋焊接一个正三棱柱形状的广告牌支架,则该三棱柱的侧面积的最大值是6.分析 用底面边长表示出高,代入侧面积公式,利用基本不等式得出最大值.
解答 解:设正三棱柱广告支架底面边长为a,高为b,则6a+3b=12,即2a+b=4,
∴正三棱柱的侧面积S=3ab=3a(4-2a)=$\frac{3}{2}$•2a(4-2a)≤$\frac{3}{2}$•($\frac{2a+4-2a}{2}$)2=6.
当且仅当2a=4-2a即a=1时,取等号.
故答案为:6.
点评 本题考查了柱体的侧面积计算,属于中档题.

练习册系列答案
相关题目
6.第96届(春季)全国糖酒商品交易会于2017年3月23日至25日在四川举办.展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系,在交易会前查阅了最近5次交易会的参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下数据:
(Ⅰ)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$))
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$))
10.二元线性方程组$\left\{\begin{array}{l}{x+5y=0}\\{2x+3y=4}\end{array}\right.$的系数矩阵D=( )
| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
8.已知函数f(x)=$\frac{4}{3}$x3-2kx2-x+1有两个不同的极值点x1,x2(x1<1<x2),若g(x)=$\frac{2x-k}{{x}^{2}+1}$,且x∈[1,x2]时,g(x)≥$\frac{k}{2}$恒成立,则实数k的取值范围是( )
| A. | ($\frac{3}{4}$,+∞) | B. | [1,+∞) | C. | ($\frac{3}{4}$,1] | D. | {1} |
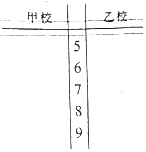 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:


 调查某学校学生的课外活动情况,制成等高条形图如图所示,则有较大把握判断:该校学生课外喜欢体育活动还是文娱活动与性别有(填“有”或“无”)关.
调查某学校学生的课外活动情况,制成等高条形图如图所示,则有较大把握判断:该校学生课外喜欢体育活动还是文娱活动与性别有(填“有”或“无”)关.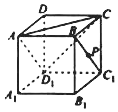 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动.则下列四个命题: