题目内容
5.设函数f(x)=x-$\frac{1}{x}$,g(x)=lnx.(Ⅰ)求函数y=2f(x)-5g(x)的单调区间;
(Ⅱ)记过函数y=f(x)-mg(x)两个极值点A,B的直线的斜率为h(m),问函数y=h(m)+2m-2是否存在零点,请说明理由.
分析 (1)求导,根据导数与函数单调性的关系,即可求得函数的单调区间;
(2)求导,构造辅助函数,根据二次函数的性质及韦达定理,求得直线AB斜率,由题意函数存在零点即$\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}=2$有解,两根均为正且x1x2=1,设$q(x)=x-\frac{1}{x}-lnx$,求导,q(x)在区间(1,+∞)上单调递增,q(x)>q(1)=0,则函数y=h(m)+2m-2没有零点.
解答 解:(Ⅰ)$y=2f(x)-5g(x)=2x-\frac{2}{x}-5lnx$,x>0,求导$y'=2+\frac{2}{x^2}-\frac{5}{x}=\frac{{2{x^2}-5x+2}}{x^2}=\frac{(2x-1)(x-2)}{x^2}$,
令y′=0,解得:x=$\frac{1}{2}$,或x=2,
当y′>0,解得:0<x<$\frac{1}{2}$,或x>2,当y′<0,解得:$\frac{1}{2}$<x<2,…(3分)
∴函数y=2f(x)-5g(x)在$(0,\frac{1}{2})$上递增,在$[\frac{1}{2},2]$上递减,在(2,+∞)上递增.…(5分)
(Ⅱ)$y=f(x)-mg(x)=x-\frac{1}{x}-mlnx(x>0)$,$y'=\frac{{{x^2}-mx+1}}{x^2}$,
设p(x)=x2-mx+1,设两个极值点A(x1,y1),B(x2,y2),…(6分)
∵函数有两个大于零极值点,
∴△=m2-4>0,得m>2且x1+x2=m,x1x2=1,
AB斜率$k=h(m)=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}$=$\frac{{{x_2}-\frac{1}{x_2}-mln{x_2}-{x_1}+\frac{1}{x_1}+mln{x_1}}}{{{x_2}-{x_1}}}=2-m\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$…(8分)
$y=h(m)+2m-2=2-m\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}+2m-2=2m-m\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}$,
由题意函数存在零点即$\frac{{ln{x_1}-ln{x_2}}}{{{x_1}-{x_2}}}=2$有解,两根均为正且x1x2=1,…(9分)
若x1<x2,则0<x1<1,x2>1,消元得$ln\frac{1}{x_2}-ln{x_2}=\frac{2}{x_2}-2{x_2}$整理得${x_2}-\frac{1}{x_2}-ln{x_2}=0$
令$q(x)=x-\frac{1}{x}-lnx$,则$q'(x)=1+\frac{1}{x^2}-\frac{1}{x}=\frac{{{x^2}-x+1}}{x^2}≥0$,
∴q(x)在区间(1,+∞)上单调递增,
∴q(x)>q(1)=0,
∴函数y=h(m)+2m-2没有零点.…(12分)
点评 本题考查导数的综合应用,导数与函数单调性及极值的关系,考查导数的几何意义,利用导数求函数切线方程,函数零点的判断,考查转化思想,属于中档题.

表1
| 停车距离d(米) | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] |
| 频数 | 26 | a | b | 8 | 2 |
| 平均每毫升血液酒精含量x毫克 | 10 | 30 | 50 | 70 | 90 |
| 平均停车距离y米 | 30 | 50 | 60 | 70 | 90 |
(Ⅰ)求a,b的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表2的数据计算y关于x的回归方程$\hat y=\hat bx+\hat a$;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”y大于(Ⅰ)中无酒状态下的停车距离平均数的3倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线$\hat y=\hat bx+\hat a$的斜率和截距的最小二乘估计分别为$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2}-n{{\bar x}^2}}}$,$\hat a=\bar y-\hat b\bar x$.)
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
| A. | $(\begin{array}{l}{0}&{5}\\{3}&{4}\end{array})$ | B. | $(\begin{array}{l}{1}&{0}\\{2}&{3}\end{array})$ | C. | $(\begin{array}{l}{1}&{5}\\{2}&{3}\end{array})$ | D. | $(\begin{array}{l}{1}&{0}\\{2}&{4}\end{array})$ |
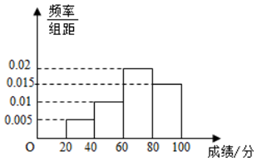 随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900.
随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为900. (1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域; 如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°
如图,在平面四边形ABCD中,AB=2,AD=$\sqrt{6}$$+\sqrt{2}$,BC=2$\sqrt{3}$,∠ABC=120°,∠DAB=75°