题目内容
已知ξ的分布列为:
若η=aξ+b,且Eη=1,Dη=2,则ab的值为 .
| ξ | 0 | 1 | 2 | ||||
| P | m |
|
|
考点:离散型随机变量及其分布列
专题:概率与统计
分析:利用ξ的分布列,先求出Eξ和Dξ,再由η=aξ+b,且Eη=1,Dη=2,利用数学期望和方差的性质,列出方程组,能求出a,b,由此能求出结果.
解答:
解:∵m=1-
-
=
,
∴由ξ的分布列知Eξ=0×
+1×
+2×
=1,
Eξ2=0×
+1×
+4×
=
,
Dξ=
-12=
,
∵η=aξ+b,且Eη=1,Dη=2,
∴Eη=aEξ+b=a+b=1,
Dη=a2Dξ=
a2=2,
解得
,或
,
∴ab=-2,或ab=-6.
故答案为:-2,或-6.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴由ξ的分布列知Eξ=0×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
Eξ2=0×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
Dξ=
| 3 |
| 2 |
| 1 |
| 2 |
∵η=aξ+b,且Eη=1,Dη=2,
∴Eη=aEξ+b=a+b=1,
Dη=a2Dξ=
| 1 |
| 2 |
解得
|
|
∴ab=-2,或ab=-6.
故答案为:-2,或-6.
点评:本题考查离散型随机变量的分布列的性质,离散型随机变量的期望与方差的计算公式,选修2-3教材P68A组第1,2题改编,中档题.

练习册系列答案
相关题目
设全体实数集为R,M={1,2},N={1,2,3,4},则(∁RM)∩N等于( )
| A、{4} |
| B、{3,4} |
| C、{2,3,4} |
| D、{1,2,3,4} |
已知A(-2,-2),B(4,2),点P在圆x2+y2=1上运动,则|PA|2+|PB|2的最大值是( )
| A、28 | B、30 | C、32 | D、34 |
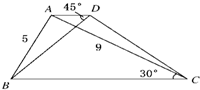 如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为
如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为