题目内容
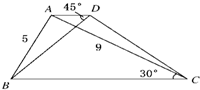如图所示，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．则BD的长为考点：余弦定理,正弦定理
专题：解三角形
分析：作 AE⊥BC，DF⊥BC，E、F为垂足，解直角三角形AEC，求得AE=
AC=DF的值．再解直角三角形DBF，求得BD=
的值．
| 1 |
| 2 |
| DF |
| sin45° |
解答：
解：过点A、D，作 AE⊥BC，DF⊥BC，E、F为垂足，则由梯形ABCD中，AD∥BC，
可得 AE=DF，都是梯形的高．
直角三角形AEC中，∵∠ACB=30°，∴AE=
AC=
=DF．
直角三角形DBF中，∵∠DBC=45°，∴BD=
=
．
可得 AE=DF，都是梯形的高．
直角三角形AEC中，∵∠ACB=30°，∴AE=
| 1 |
| 2 |
| 9 |
| 2 |
直角三角形DBF中，∵∠DBC=45°，∴BD=
| DF |
| sin45° |
9
| ||
| 2 |
点评：本题主要考查直角三角形中的边角关系，作出辅助线，是解题的关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
佛山某中学高三（1）班排球队和篮球队各有10名同学，现测得排球队10人的身高（单位：cm）分别是：162、170、171、182、163、158、179、168、183、168，篮球队10人的身高（单位：cm）分别是：170、159、162、173、181、165、176、168、178、179．在等比数列{an}中，an＞0，若a1a2a3…a2012=22012，则a2a2011=（ ）
| A、2 |
| B、4 |
| C、21005 |
| D、21006 |