题目内容
2.下列命题中的假命题是( )| A. | ?x∈R,x3<0 | |
| B. | 在斜二测画法中,直观图的面积是原图形面积的4$\sqrt{2}$ | |
| C. | “a>0”是“|a|>0”充分不必要的条件 | |
| D. | 关于x的不等式x2-2ax-8a2<0(a>0)的解集为(x1,x2),且x2-x1=15,则$a=\frac{5}{2}$ |
分析 根据条件分别判断每个命题的真假关系即可得到结论.
解答 解:A.当x=-1时,x3<0成立,故A是真命题.
B.在斜二测画法中,直观图的面积是原图形面积的$\frac{\sqrt{2}}{4}$,故B是假命题.
C.由|a|>0得a>0或a<0,则“a>0”是“|a|>0”充分不必要的条件,故C是真命题.
D.∵不等式x2-2ax-8a2<0(a>0)等价为(x-2a)(x-4a)<0,
∴不等式的解集为(2a,4a),
即x1=2a,x2=4a,
∵x2-x1=15,
∴4a-2a=2a=15,
∴$a=\frac{5}{2}$,故D是真命题.
故选:B
点评 本题主要考查命题的真假判断,根据条件分别进行判断是解决本题的关键.

练习册系列答案
相关题目
10.已知点P是抛物线y2=2x上的一个动点,则点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与点P到y轴的距离之和的最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
17.下列命题中,错误的是( )
| A. | 一条直线与两个平行平面中的一个相交,则必与另一个相交 | |
| B. | 平行于同一个平面的两个平面平行 | |
| C. | 一个平面与两个平行平面相交,交线平行 | |
| D. | 平行于同一条直线的两个平面平行 |
7.命题“存在x0∈R使得2${\;}^{{x}_{0}}$≤1”的否定是( )
| A. | 不存在x0∈R使得2${\;}^{{x}_{0}}$>0 | B. | 存在x0∈R使得2${\;}^{{x}_{0}}$>0 | ||
| C. | 对任意x∈R,2x>0 | D. | 对任意x∈R,2x≤0 |
12.执行如图所示程序框图,若输入的m,n分别为18,30,则输出的结果是( )

| A. | 0 | B. | 2 | C. | 6 | D. | 18 |
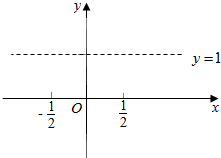 已知直线y=1与曲线y=x2-|x|+a有四个交点.
已知直线y=1与曲线y=x2-|x|+a有四个交点.