题目内容
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
考点:点与圆的位置关系
专题:计算题
分析:由二元二次方程表示圆的条件得到m的不等式,又圆心到圆点的距离应大于半径,解不等式即可得到结果.
解答:
解:方程x2+y2-x+y+m=0表示一个圆,
则1+1-4m>0,
∴m<
,
x2+y2-x+y+m=0,
则有(x-
)2+(y+
)2=
-m,
要满足条件,则有圆心到圆点的距离应大于半径,即
>
,
>
-m,
即m>0,
故选:A.
则1+1-4m>0,
∴m<
| 1 |
| 2 |
x2+y2-x+y+m=0,
则有(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要满足条件,则有圆心到圆点的距离应大于半径,即
(
|
|
| 1 |
| 2 |
| 1 |
| 2 |
即m>0,
故选:A.
点评:本题考查二元二次方程表示圆的条件,属基础知识的考查,本题解题的关键是看清楚所表示的二元二次方程的各个系数之间的关系.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、x2-
| ||||
B、
| ||||
C、
| ||||
D、
|
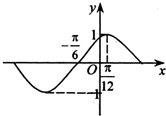 函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<
函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<| π |
| 2 |
| π |
| 4 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|