题目内容
某三棱锥的三视图如图所示,该三棱锥的体积为 .


考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图及题设条件知,此几何体为一个三棱锥,其高为3,底面是直角边长为3,4的直角三角形,故先求出底面积,再由体积公式求解其体积即可.
解答:
解:由题设条件,此几何几何体为一个三棱锥,
其高为3,底面是直角边长为3,4的直角三角形,
故其体积是
×
×3×4×4=8,
故答案为:8
其高为3,底面是直角边长为3,4的直角三角形,
故其体积是
| 1 |
| 3 |
| 1 |
| 2 |
故答案为:8
点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线y=(a-a2)x-2和y=(3a+1)x+1互相平行,则a的值等于( )
| A、2 | B、1 | C、0 | D、-1 |
已知两条不同的直线a,b和平面α,那么下列命题中的真命题是( )
| A、若a⊥b,b⊥α,则a∥α |
| B、若a∥α,b∥α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a∥b,b∥α,则a∥α |
复数
等于( )
| 3+i |
| 1+i |
| A、1+2i | B、1-2i |
| C、2-i | D、2+i |
如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是( )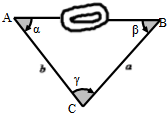

| A、α,a,b |
| B、α,β,a |
| C、a,b,γ |
| D、α,β,b |
若实数x、y满足不等式组
则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |
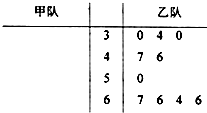 甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):