题目内容
若a+b=1（其中a＞0，b＞0），则
+
的最小值等于 ．
| 1 |
| a |
| 2 |
| b |
考点：基本不等式
专题：不等式的解法及应用
分析：根据
+
=
+
=3+
+
，利用基本不等式求得
+
的最小值．
| 1 |
| a |
| 2 |
| b |
| a+b |
| a |
| 2a+2b |
| b |
| b |
| a |
| 2a |
| b |
| 1 |
| a |
| 2 |
| b |
解答：
解：∵a+b=1（其中a＞0，b＞0），
∴
+
=
+
=3+
+
≥3+2
，
当且仅当
=
时，取等号，
故
+
的最小值等于3+2
，
故答案为：3+2
．
∴
| 1 |
| a |
| 2 |
| b |
| a+b |
| a |
| 2a+2b |
| b |
| b |
| a |
| 2a |
| b |
| 2 |
当且仅当
| b |
| a |
| 2a |
| b |
故
| 1 |
| a |
| 2 |
| b |
| 2 |
故答案为：3+2
| 2 |
点评：本题主要考查了基本不等式在最值问题中的应用，考查了学生对基本不等式的整体把握和灵活运用，属于基础题．
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
已知函数f（x）=
下列是关于函数y=f[f（x）]+1的零点个数的4个判断：
①当k＞0时，有3个零点；
②当k＜0时，有2个零点；
③当k＞0时，有4个零点；
④当k＜0时，有1个零点．
则正确的判断是（ ）
|
①当k＞0时，有3个零点；
②当k＜0时，有2个零点；
③当k＞0时，有4个零点；
④当k＜0时，有1个零点．
则正确的判断是（ ）
| A、①④ | B、②③ | C、①② | D、③④ |
若P是两条异面直线l，m外的任意一点，则下列命题：
①过点P有且只有一条直线与l，m都平行；
②过点P有且只有一条直线与l，m都垂直；
③过点P有且只有一条直线与l，m都相交；
④过点P有且只有一条直线与l，m都异面．
其中假命题的个数为（ ）
①过点P有且只有一条直线与l，m都平行；
②过点P有且只有一条直线与l，m都垂直；
③过点P有且只有一条直线与l，m都相交；
④过点P有且只有一条直线与l，m都异面．
其中假命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
在复平面内，复数z=
（i为虚数单位）的共轭复数等于（ ）
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |
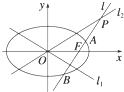已知椭圆C的方程为