题目内容
已知动点P与平面上两定点A(-
,0),B(
,0)连线的斜率的积为定值-
.
(1)求点P的轨迹方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
| 3 |
| 3 |
| 1 |
| 3 |
(1)求点P的轨迹方程;
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设动点P(x,y),由已知条件推导出
•
=-
,由此能求出曲线的方程.
(2)假若存在这样的k值,由
,得(1+3k2)x2+12kx+9=0.由此利用根的判别式和韦达定理能求出存在k=
,使得以CD为直径的圆过点E.
| y | ||
x+
|
| y | ||
x-
|
| 1 |
| 3 |
(2)假若存在这样的k值,由
|
| 7 |
| 6 |
解答:
解:(1)设动点P(x,y),
∵动点P与平面上两定点A(-
,0),B(
,0)连线的斜率的积为定值-
,
∴
•
=-
,x≠±
,
整理,得:x2+3y2=3,x≠±
,
∴所求曲线的方程为
+y2=1.(x≠±
)
(2)假若存在这样的k值,
由
,得(1+3k2)x2+12kx+9=0.
∴△=(12k)2-36(1+3k2)>0.①
设C(x1,y1)、D(x2,y2),
则
,②
而y1•y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4.
要使以CD为直径的圆过点E(-1,0),
当且仅当CE⊥DE,
∴
•
=-1,即y1y2+(x1+1)(x2+1)=0.
∴(k2+1)x1x2+2(k+1)(x1+x2)+5=0.③
将②式代入③整理,解得k=
.
经验证,k=
,使①成立.
综上可知,存在k=
,使得以CD为直径的圆过点E.
∵动点P与平面上两定点A(-
| 3 |
| 3 |
| 1 |
| 3 |
∴
| y | ||
x+
|
| y | ||
x-
|
| 1 |
| 3 |
| 3 |
整理,得:x2+3y2=3,x≠±
| 3 |
∴所求曲线的方程为
| x2 |
| 3 |
| 3 |
(2)假若存在这样的k值,
由
|
∴△=(12k)2-36(1+3k2)>0.①
设C(x1,y1)、D(x2,y2),
则
|
而y1•y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4.
要使以CD为直径的圆过点E(-1,0),
当且仅当CE⊥DE,
∴
| y1 |
| x1+1 |
| y2 |
| x2+1 |
∴(k2+1)x1x2+2(k+1)(x1+x2)+5=0.③
将②式代入③整理,解得k=
| 7 |
| 6 |
经验证,k=
| 7 |
| 6 |
综上可知,存在k=
| 7 |
| 6 |
点评:本题考查点的轨迹方程的求法,考查是否存在k的值,使以CD为直径的圆过E点的判断,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
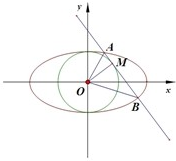 如图,已知椭圆C的方程为
如图,已知椭圆C的方程为 如图,点P(0,-1)是椭圆
如图,点P(0,-1)是椭圆