题目内容
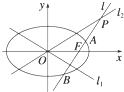 已知椭圆C的方程为
已知椭圆C的方程为| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)若l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程及离心率;
(2)求
| FA |
| AP |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(1)由题意,先由双曲线的性质得出a,b所满足的关系式a=
b,再与a2+b2=22联立求出两者的值即可得出椭圆的方程;
(2)由题意,联立l与l2的方程求出它们的交点P点的坐标,再令
=λ,利用引入的参数表示出点A的坐标,由于点A在椭圆上,代入椭圆的方程结合椭圆的性质求出λ的取值范围,即可得出所求的最大值.
| 3 |
(2)由题意,联立l与l2的方程求出它们的交点P点的坐标,再令
| FA |
| AP |
解答:
解:(1)双曲线的渐近线为y=±
x,两渐近线夹角为60°,又
<1,∴∠POx=30°,
∴
=tan 30°=
,∴a=
b.又a2+b2=22,
∴3b2+b2=4,
∴b2=1,a2=3,∴椭圆C的方程为
+y2=1,
∴离心率e=
=
.
(2)由已知,l:y=
(x-c)与y=
x联立,
解方程组得P(
,
).
设
=λ,则
=λ
,∵F(c,0),设A(x0,y0),
则(x0-c,y0)=λ(
-x0,
-y0),
∴x0=
,y0=
.即A(
,
).
将A点坐标代入椭圆方程,得(c2+λa2)2+λ2a4=(1+λ)2a2c2,
等式两边同除以a4,(e2+λ)2+λ2=e2(1+λ)2,e∈(0,1),
∴λ2=
=-[2-e2+
]+3≤-2
+3=3-2
=(
-1)2,
∴当2-e2=
,即e2=2-
时,λ有最大值
-1,即
的最大值为
-1.
| b |
| a |
| b |
| a |
∴
| b |
| a |
| ||
| 3 |
| 3 |
∴3b2+b2=4,
∴b2=1,a2=3,∴椭圆C的方程为
| x2 |
| 3 |
∴离心率e=
| ||
| a |
| ||
| 3 |
(2)由已知,l:y=
| a |
| b |
| b |
| a |
解方程组得P(
| a2 |
| c |
| ab |
| c |
设
| FA |
| AP |
| FA |
| AP |
则(x0-c,y0)=λ(
| a2 |
| c |
| ab |
| c |
∴x0=
c+λ×
| ||
| 1+λ |
λ×
| ||
| 1+λ |
c+λ×
| ||
| 1+λ |
λ×
| ||
| 1+λ |
将A点坐标代入椭圆方程,得(c2+λa2)2+λ2a4=(1+λ)2a2c2,
等式两边同除以a4,(e2+λ)2+λ2=e2(1+λ)2,e∈(0,1),
∴λ2=
| e4-e2 |
| e2-2 |
| 2 |
| 2-e2 |
(2-e2)×
|
| 2 |
| 2 |
∴当2-e2=
| 2 |
| 2 |
| 2 |
| FA |
| AP |
| 2 |
点评:本题考查直线与圆锥曲线的综合问题,此类题运算量大,综合性强,容易出错,解答时要严谨,避免变形出错导致解题失败

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设函数f(x)=
的定义域为M,函数g(x)=lg(1+x)的定义域为N,则( )
| 1 | ||
|
| A、M∩N=(-1,1] |
| B、M∩N=R |
| C、∁RM=[1,+∞) |
| D、∁RN=(-∞,-1) |
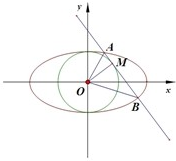 如图,已知椭圆C的方程为
如图,已知椭圆C的方程为 如图,点P(0,-1)是椭圆
如图,点P(0,-1)是椭圆