题目内容
一只蚂蚁在边长为4的正三角形区域内随机爬行,则其恰在离三个顶点的距离都大于1的地方的概率为 .
考点:几何概型
专题:概率与统计
分析:先求出三角形的面积,再求出据三角形的三顶点距离小于等于1的区域为三个扇形,求出扇形的面积,利用几何概型概率公式求出恰在离三个顶点距离都大于1的地方的概率.
解答:
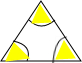 解:小蚂蚁活动的范围是在三角形的内部,三角形的边长为4正三角形,所以面积为
解:小蚂蚁活动的范围是在三角形的内部,三角形的边长为4正三角形,所以面积为
×
•4×4=4
,
而“恰在离三个顶点距离都大于1”正好是三角形去掉三个半径为1,圆心角为
的扇形,面积为3×
×
•12=
,
所以恰在离三个顶点距离都大于1的地方的概率为
=1-
.
故答案为:1-
π.
 解:小蚂蚁活动的范围是在三角形的内部,三角形的边长为4正三角形,所以面积为
解:小蚂蚁活动的范围是在三角形的内部,三角形的边长为4正三角形,所以面积为| 1 |
| 2 |
| ||
| 2 |
| 3 |
而“恰在离三个顶点距离都大于1”正好是三角形去掉三个半径为1,圆心角为
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
所以恰在离三个顶点距离都大于1的地方的概率为
4
| ||||
4
|
| ||
| 24 |
故答案为:1-
| ||
| 24 |
点评:本题主要考查几何概型概率公式、对立事件概率公式、三角形的面积公式、圆的面积公式,属于中档题.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,若目标函数z=y+ax仅在点(5,3)处取得最小值,则实数a的取值范围为( )
|
| A、(-∞,-1) | ||
| B、(0,+∞) | ||
C、(
| ||
| D、(1,+∞) |
 如图,点P(0,-1)是椭圆
如图,点P(0,-1)是椭圆