题目内容
在等比数列{an}中,am=10k,ak=10m,则am+k= .
考点:等比数列的性质
专题:等差数列与等比数列
分析:利用等比数列的性质,可求得其公比q=
,利用am+k=am•qk即可求得答案.
| 1 |
| 10 |
解答:
解:在等比数列{an}中,∵am=10k,ak=10m,
∴qm-k=
=10k-m=(
)m-k,
∴q=
,
∴am+k=am•qk=10k•(
)k=1.
故答案为:1.
∴qm-k=
| am |
| ak |
| 1 |
| 10 |
∴q=
| 1 |
| 10 |
∴am+k=am•qk=10k•(
| 1 |
| 10 |
故答案为:1.
点评:本题考查等比数列的性质,求得其公比q=
是关键,属于中档题.
| 1 |
| 10 |

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
把18化为二进制数为( )
| A、10010(2) |
| B、10110(2) |
| C、11010(2) |
| D、10011(2) |
等差数列{an}的前n项和为Sn,若a1+a9=6,则S9的值是( )
| A、25 | B、26 | C、27 | D、28 |
已知函数f(x)=x2-2ax+b,则“1<a<2”是“f(1)<f(3)”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
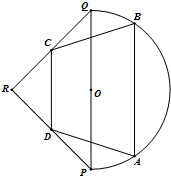 如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.
如图,我市有一个健身公园,由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成,其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD,按实际需要,四边形ABCD的两个顶点C、D分别在线段QR、PR上,另外两个顶点A、B在半圆上,AB∥CD∥PQ,且AB、CD间的距离为1km.设四边形ABCD的周长为ckm.