题目内容
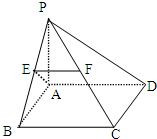 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.(Ⅰ)求证:AE⊥PC;
(Ⅱ)求点A到平面PBD的距离.
考点:直线与平面垂直的性质,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(Ⅰ)由等腰三角形性质得AE⊥PB,由线面垂直得PA⊥BC,从而得到BC⊥平面PAB,所以AE⊥BC,从而得到AE⊥平面PBC,由此能证明AE⊥PC.
(Ⅱ)设点A到平面PBD的距离为d,利用等积法能求出点A到平面PBD的距离为
.
(Ⅱ)设点A到平面PBD的距离为d,利用等积法能求出点A到平面PBD的距离为
| ||
| 3 |
解答:
 (本小题12分)
(本小题12分)
(Ⅰ)证明:∵AP=AB,E是PB的中点,∴AE⊥PB,
∵PA⊥平面ABCD,∴PA⊥BC,
∵AB⊥BC且PA∩AB=A
∴BC⊥平面PAB,∵AE?平面PAB,
∴AE⊥BC,∵PB∩BC=B,
∴AE⊥平面PBC,∴AE⊥PC.…(6分)
(Ⅱ)解:设点A到平面PBD的距离为d,利用体积法,
VP-ABD=VA-PBD⇒
S△ABD•PA=
S△PBD•d⇒d=
,
∴点A到平面PBD的距离为
.…(12分)
 (本小题12分)
(本小题12分)(Ⅰ)证明:∵AP=AB,E是PB的中点,∴AE⊥PB,
∵PA⊥平面ABCD,∴PA⊥BC,
∵AB⊥BC且PA∩AB=A
∴BC⊥平面PAB,∵AE?平面PAB,
∴AE⊥BC,∵PB∩BC=B,
∴AE⊥平面PBC,∴AE⊥PC.…(6分)
(Ⅱ)解:设点A到平面PBD的距离为d,利用体积法,
VP-ABD=VA-PBD⇒
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
∴点A到平面PBD的距离为
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x3+ax+1是R上的单调递增函数,则a的取值范围是( )
| A、a≥0 | B、a≥-1 |
| C、a<0 | D、a<-1 |
若抛物线C1:y2=4x的焦点F恰好是双曲线C2:
-
=1(a>0,b>0)的右焦点,且C1与C2交点的连线过点F,则双曲线C2的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、2
| ||||||
C、3+2
| ||||||
D、
|