题目内容
已知数列{an}的前n项和为Sn,且Sn=n2-8n,令bn=|an|.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn的表达式.
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn的表达式.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)当n≥2时,易求an=Sn-Sn-1=2n-9,当n=1时,a1=-7=S1,满足题设,从而可得数列{an}的通项公式;
(2)由bn=|an|,易知当1≤n≤4或n>4时,数列bn是等差数列,从而利用等差数列的求和公式即可求得数列{bn}的前n项和Tn的表达式.
(2)由bn=|an|,易知当1≤n≤4或n>4时,数列bn是等差数列,从而利用等差数列的求和公式即可求得数列{bn}的前n项和Tn的表达式.
解答:
解:(1)当n≥2时,an=Sn-Sn-1=(n2-8n)-[(n-1)2-8(n-1)]=2n-9,
当n=1时,a1=-7=S1,满足题设,
∴an=2n-9;
(2)∵bn=|an|=
,
∴当1≤n≤4或n>4时,数列bn是等差数列,
∴当1≤n≤4时,Tn=-Sn=8n-n2;
当n≥5时,Tn=-(a1+a2+a3+a4)+(a5+a6+…+an)
=-S4+(Sn-S4)
=Sn-2S4
=n2-8n-2(42-8×4)
=n2-8n+32.
∴Tn=
.
当n=1时,a1=-7=S1,满足题设,
∴an=2n-9;
(2)∵bn=|an|=
|
∴当1≤n≤4或n>4时,数列bn是等差数列,
∴当1≤n≤4时,Tn=-Sn=8n-n2;
当n≥5时,Tn=-(a1+a2+a3+a4)+(a5+a6+…+an)
=-S4+(Sn-S4)
=Sn-2S4
=n2-8n-2(42-8×4)
=n2-8n+32.
∴Tn=
|
点评:本题考查数列的求和,着重考查等差关系的确定及通项公式、求和公式的应用,考查分类讨论思想与运算求解能力的运用,属于中档题.

练习册系列答案
相关题目
设a>0,b>0则下列不等中不恒成立的是( )
A、a+
| ||||||
| B、a2+b2≥2(a+b-1) | ||||||
C、
| ||||||
| D、a3+b3≥2ab2 |
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为原点,若|FE|=|EP|,则双曲线离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
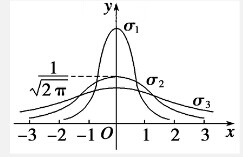 如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )| A、σ1>1>σ2>σ3>0 |
| B、0<σ1<σ2<1<σ3 |
| C、σ1>σ2>1>σ3>0 |
| D、0<σ1<σ2=1<σ3 |
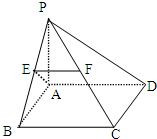 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.