题目内容
已知函数f(x)=x3-x2,x∈R
(1)若正数m,n满足m•n>1,证明:f(m),f(n)至少有一个不小于零;
(2)若a,b为不相等的正实数且满足f(a)=f(b),求证a+b<
.
(1)若正数m,n满足m•n>1,证明:f(m),f(n)至少有一个不小于零;
(2)若a,b为不相等的正实数且满足f(a)=f(b),求证a+b<
| 4 |
| 3 |
考点:反证法
专题:证明题
分析:(1)假设f(m)<0,f(n)<0即m3-m2<0,n3-n2<0,得mn<1这与m,n>1矛盾,从而f(m),f(n)至少有一个不小于零.
(2)证明:由f(a)=f(b)得a3-a2=b3-b2,(a-b)(a2+ab+b2)=(a-b)(a+b),从而(a+b)2-(a+b)=ab<(
)2,进而a+b<
.
(2)证明:由f(a)=f(b)得a3-a2=b3-b2,(a-b)(a2+ab+b2)=(a-b)(a+b),从而(a+b)2-(a+b)=ab<(
| a+b |
| 2 |
| 4 |
| 3 |
解答:
解:(1)证明:假设f(m)<0,f(n)<0
即m3-m2<0,n3-n2<0
∵m>0,n>0
∴m-1<0 n-1<0
∴0<m<1,0<n<1,
∴mn<1这与m,n>1矛盾
∴假设不成立,即f(m),f(n)至少有一个不小于零.
(2)证明:由f(a)=f(b)得a3-a2=b3-b2,
∴a3-b3=a2-b2
∴(a-b)(a2+ab+b2)=(a-b)(a+b)
∵a≠b∴a2+ab+b2=a+b,
∴(a+b)2-(a+b)=ab<(
)2
∴
(a+b)2-(a+b)<0,
∴a+b<
即m3-m2<0,n3-n2<0
∵m>0,n>0
∴m-1<0 n-1<0
∴0<m<1,0<n<1,
∴mn<1这与m,n>1矛盾
∴假设不成立,即f(m),f(n)至少有一个不小于零.
(2)证明:由f(a)=f(b)得a3-a2=b3-b2,
∴a3-b3=a2-b2
∴(a-b)(a2+ab+b2)=(a-b)(a+b)
∵a≠b∴a2+ab+b2=a+b,
∴(a+b)2-(a+b)=ab<(
| a+b |
| 2 |
∴
| 3 |
| 4 |
∴a+b<
| 4 |
| 3 |
点评:本题考察了不等式的证明,考察了反证法的证明问题,是一道中档题.

练习册系列答案
相关题目
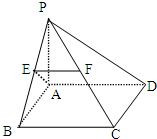 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.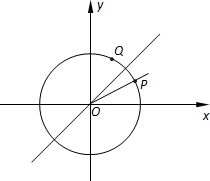 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=