题目内容
已知函数f(x)=ax+
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)用a表示出b,c;
(2)证明:当a≥
时,f(x)≥1nx在[1,+∞)上恒成立;
(3)证明:1+
+
+…+
>1n(n+1)+
.(n∈N*)
| b |
| x |
(1)用a表示出b,c;
(2)证明:当a≥
| 1 |
| 2 |
(3)证明:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| n |
| 2(n+1) |
考点:数列的求和,利用导数研究曲线上某点切线方程
专题:等差数列与等比数列
分析:(1)由已知条件利用导数性质得
,由此能求出
.
(2)令g(x)=f(x)-lnx=ax+
+1-2a-lnx,则g′(x)=a-
-
=
,由此能证明当a≥
时,f(x)≥lnx在[1,+∞)上恒成立.
(3)由已知条件推导出ln(k+1)-lnk<
(
+
),令k=1,2,…,n,得n个不等式,将其累加,能证明1+
+
+…+
>1n(n+1)+
.(n∈N*)
|
|
(2)令g(x)=f(x)-lnx=ax+
| a-1 |
| x |
| a-1 |
| x2 |
| 1 |
| x |
a(x+
| ||
| x2 |
| 1 |
| 2 |
(3)由已知条件推导出ln(k+1)-lnk<
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| n |
| 2(n+1) |
解答:
(1)解:∵f(x)=ax+
+c,
∴f′(x)=a-
,
∵f(x)=ax+
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1,
∴
,
解得
.
(2)证明:由(1)得f(x)=ax+
+1-2a,
令g(x)=f(x)-lnx=ax+
+1-2a-lnx,x∈[1,+∞),g(1)=0,
g′(x)=a-
-
=
=
,
∵a≥
,∴
≤1,∴x>1,g′(x)>0,
g(x)是增函数,∴g(x)>g(1)=0,
即f(x)>lnx,∴x≥1时,f(x)≥lnx,
∴当a≥
时,f(x)≥lnx在[1,+∞)上恒成立.
(3)证明:由(2)知,当a≥
时,有f(x)≥lnx,x≥1,
令a=
,则f(x)=
(x-
)≥lnx,
当且仅当x=1时,“=”成立,即当x>1时,总有
(x-
)>lnx,
令x=
,则
<
(
-
)=
(
+
),
即ln(k+1)-lnk<
(
+
),
令k=1,2,…,n,得n个不等式,
将其累加,得:
ln(n+1)<
+(
+
+…+
)+
,
∴1+
+
+…+
>1n(n+1)+
.(n∈N*)
| b |
| x |
∴f′(x)=a-
| b |
| x2 |
∵f(x)=ax+
| b |
| x |
∴
|
解得
|
(2)证明:由(1)得f(x)=ax+
| a-1 |
| x |
令g(x)=f(x)-lnx=ax+
| a-1 |
| x |
g′(x)=a-
| a-1 |
| x2 |
| 1 |
| x |
=
| (ax+a-1)(x-1) |
| x2 |
=
a(x+
| ||
| x2 |
∵a≥
| 1 |
| 2 |
| 1-a |
| a |
g(x)是增函数,∴g(x)>g(1)=0,
即f(x)>lnx,∴x≥1时,f(x)≥lnx,
∴当a≥
| 1 |
| 2 |
(3)证明:由(2)知,当a≥
| 1 |
| 2 |
令a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
当且仅当x=1时,“=”成立,即当x>1时,总有
| 1 |
| 2 |
| 1 |
| x |
令x=
| k+1 |
| k |
| k+1 |
| k |
| 1 |
| 2 |
| k+1 |
| k |
| k |
| k+1 |
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
即ln(k+1)-lnk<
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
令k=1,2,…,n,得n个不等式,
将其累加,得:
ln(n+1)<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2(n+1) |
∴1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| n |
| 2(n+1) |
点评:本题考查不等式的证明,解题时要认真审题,注意导数性质、累加求和等知识点的合理运用.

练习册系列答案
相关题目
不等式x(9-x)>0的解集是( )
| A、{x|x>0或x<9} |
| B、{x|x<0或x>9} |
| C、{x|0<x<9} |
| D、{x|-9<x<0} |
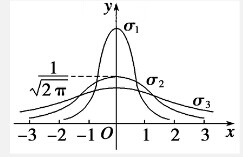 如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )| A、σ1>1>σ2>σ3>0 |
| B、0<σ1<σ2<1<σ3 |
| C、σ1>σ2>1>σ3>0 |
| D、0<σ1<σ2=1<σ3 |
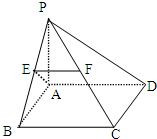 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.