题目内容
已知函数f（x）=x3+ax+1是R上的单调递增函数，则a的取值范围是（ ）
| A、a≥0 | B、a≥-1 |
| C、a＜0 | D、a＜-1 |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，根据条件得到f′（x）≥0恒成立，即可得到结论．
解答：
解：∵函数f（x）=x3+ax+1是R上的单调递增函数，
∴f′（x）=3x2+a≥0恒成立，
即a≥-3x2，
∵-3x2≤0，∴a≥0，
故选：A
∴f′（x）=3x2+a≥0恒成立，
即a≥-3x2，
∵-3x2≤0，∴a≥0，
故选：A
点评：本题主要考查函数单调性和导数之间的关系，考查恒成立问题．比较基础．
练习册系列答案
相关题目
下列函数中，周期为π且图象关于直线x=
对称的函数是（ ）
| π |
| 3 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（2x+
| ||||
C、f（x）=2sin（
| ||||
D、f（x）=2sin（2x-
|
设a＞0，b＞0则下列不等中不恒成立的是（ ）
A、a+
| ||||||
| B、a2+b2≥2（a+b-1） | ||||||
C、
| ||||||
| D、a3+b3≥2ab2 |
下列函数中，在（0，+∞）上为增函数的是（ ）
| A、f（x）=sin2x |
| B、f（x）=xex |
| C、f（x）=x3-x |
| D、f（x）=-x+lnx |
设函数f（x）=
在x=0处f（x）（ ）
|
| A、不连续 |
| B、连续，但不可导 |
| C、可导，但导数不连续 |
| D、可导，且导数连续 |
不等式x（9-x）＞0的解集是（ ）
| A、{x|x＞0或x＜9} |
| B、{x|x＜0或x＞9} |
| C、{x|0＜x＜9} |
| D、{x|-9＜x＜0} |
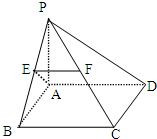如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，AP=AB=1，E，F分别是PB，PC的中点．