题目内容
已知抛物线方程为x2=4y,过点M(0,2)作直线与抛物线交于两点A(x1,y1),B(x2,y2),过A,B分别作抛物线的切线,两切线的交点为P.
(Ⅰ)求x1x2的值;
(Ⅱ)求点P的纵坐标;
(Ⅲ)求△PAB面积的最小值.
(Ⅰ)求x1x2的值;
(Ⅱ)求点P的纵坐标;
(Ⅲ)求△PAB面积的最小值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设出直线AB的方程与抛物线方程联立,利用韦达定理求得x1x2的值.
(Ⅱ)分别表示出两个切线方程,联立可求得y.
(Ⅲ)表示出点P到直线AB的距离,线段AB的长度,利用三角形面积公式表示出三角形面积,进而求得△PAB面积的最小值.
(Ⅱ)分别表示出两个切线方程,联立可求得y.
(Ⅲ)表示出点P到直线AB的距离,线段AB的长度,利用三角形面积公式表示出三角形面积,进而求得△PAB面积的最小值.
解答:
解:(Ⅰ)设直线AB的斜率为k,则直线方程为y=kx+2,与抛物线方程联立得x2-4kx-8=0,
△=16k2+32>0,
∴x1x2=-8,
(Ⅱ)由导数的几何意义知过点A的切线斜率为
,
∴切线方程为y-
=
(x-x1),①
同理过B的切线方程为y=
-
,②
由
-
=
-
,③
把③代入①得y=-2,
∴P的纵坐标为-2.
(Ⅲ)∵x1+x2=4k,x1x2=-8,
∵点P到直线AB的距离为d=
,
线段AB的长度为|x1-x2|
=
•
=4
•
,
S=
4
•
=4(k2+2)
≥8
.
当且仅当k=0时取等号,
∴三角形PAB面积最小值为8
.
△=16k2+32>0,
∴x1x2=-8,
(Ⅱ)由导数的几何意义知过点A的切线斜率为
| x1 |
| 2 |
∴切线方程为y-
| ||
| 4 |
| x1 |
| 2 |
同理过B的切线方程为y=
| x2x |
| 2 |
| ||
| 4 |
由
| x1x |
| 2 |
| ||
| 4 |
| x2x |
| 2 |
| ||
| 4 |
把③代入①得y=-2,
∴P的纵坐标为-2.
(Ⅲ)∵x1+x2=4k,x1x2=-8,
∵点P到直线AB的距离为d=
| |2k2+4| | ||
|
线段AB的长度为|x1-x2|
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| k2+2 |
| 1+k2 |
S=
| 1 |
| 2 |
| |2k2+4| | ||
|
| • |
| k2+2 |
| 1+k2 |
| 3 |
| 2 |
| 2 |
当且仅当k=0时取等号,
∴三角形PAB面积最小值为8
| 2 |
点评:本题主要考查了抛物线与直线的位置关系,点到直线距离的应用.考查了学生分析推理和运算的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,在(0,+∞)上为增函数的是( )
| A、f(x)=sin2x |
| B、f(x)=xex |
| C、f(x)=x3-x |
| D、f(x)=-x+lnx |
函数f(x)=
+
的定义域是( )
| x+3 |
| 1 |
| x+2 |
| A、{x|x≠2} |
| B、{x|x≥-3} |
| C、{x|x≥-3或x≠-2} |
| D、{x|x≥-3且x≠-2} |
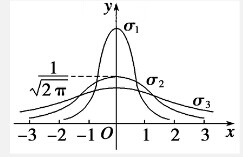 如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )| A、σ1>1>σ2>σ3>0 |
| B、0<σ1<σ2<1<σ3 |
| C、σ1>σ2>1>σ3>0 |
| D、0<σ1<σ2=1<σ3 |
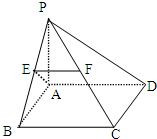 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.